Hypercube projection
16 posts
• Page 1 of 1
Hypercube projection
The vertex-first projection of a cube is a hexagon, of a tesseract is a rhombic dodecahedron. Is the projection of a penteract a 24-cell, and what follows?
- Oschkar
- Mononian
- Posts: 15
- Joined: Fri Jul 03, 2009 5:49 pm
Re: Hypercube projection
No, it's some kind of "rhombic icosachoron", a pentatopal arrangement of rhombic dodecahedra made up of four cubes. Can anyome render this for me?
- Oschkar
- Mononian
- Posts: 15
- Joined: Fri Jul 03, 2009 5:49 pm
Re: Hypercube projection
Oschkar wrote:*bump*
Hi, sorry, I've been busy, haven't had time to catch up with threads and respond.
Do you have 4D coordinates for this shape? I can render it easily if you do. Unfortunately, my program doesn't do 5D->4D projections yet, so we'll have to calculate 4D coordinates by hand.
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Hypercube projection
The vertex-first projection of the cube etc, is the 'cats-eye' polytope. symbol: m[3o]3m. repeat 3o any number of times
In two dimensions, this is a hexagon. In three dimensions, this is the rhombic dodecahedron.
In four dimensions, it has 20 rhombic sides, in five dimensions, 40 sides.
You can make these by shortening the long axis of the 'cube' until it's the same length as the edge. In this condition, the corner will fit exactly into the face of a simplex, so that N+1 surround the central vertex.
It carries the name of the cats-eye, because in N dimensions, the cat's-eye reflector corresponds to a cut across a tiling of small cubes, perpendicular to the long axis of a cube. It produces various pits in the shape of a cube-corner: light from any direction is reflected by reversal in N perpendicular axies, to return the light to where it came from, as does cat's eyes. Reflectors of this type are used along motor-car roads.
In two dimensions, this is a hexagon. In three dimensions, this is the rhombic dodecahedron.
In four dimensions, it has 20 rhombic sides, in five dimensions, 40 sides.
You can make these by shortening the long axis of the 'cube' until it's the same length as the edge. In this condition, the corner will fit exactly into the face of a simplex, so that N+1 surround the central vertex.
It carries the name of the cats-eye, because in N dimensions, the cat's-eye reflector corresponds to a cut across a tiling of small cubes, perpendicular to the long axis of a cube. It produces various pits in the shape of a cube-corner: light from any direction is reflected by reversal in N perpendicular axies, to return the light to where it came from, as does cat's eyes. Reflectors of this type are used along motor-car roads.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2014
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Hypercube projection
3/4, sqrt(15)/4, 0, 0
-3/4, -sqrt(15)/4, 0, 0
1/2, sqrt(15)/6, sqrt(30)/6, 0
1/2, -sqrt(15)/6, -sqrt(30)/6, 0
-1/2, sqrt(15)/6, sqrt(30)/6, 0
-1/2, -sqrt(15)/6, -sqrt(30)/6, 0
3/4, -sqrt(15)/12, sqrt(30)/6, 0
-3/4, sqrt(15)/12, -sqrt(30)/6, 0
1/2, sqrt(15)/6, -sqrt(30)/12, sqrt(10)/4
1/2, -sqrt(15)/6, sqrt(30)/12, sqrt(10)/4
1/2, sqrt(15)/6, -sqrt(30)/12, -sqrt(10)/4
1/2, -sqrt(15)/6, sqrt(30)/12, -sqrt(10)/4
-1/2, sqrt(15)/6, -sqrt(30)/12, sqrt(10)/4
-1/2, -sqrt(15)/6, sqrt(30)/12, sqrt(10)/4
-1/2, sqrt(15)/6, -sqrt(30)/12, -sqrt(10)/4
-1/2, -sqrt(15)/6, sqrt(30)/12, -sqrt(10)/4
3/4, -sqrt(15)/12, -sqrt(30)/12, sqrt(10)/4
3/4, -sqrt(15)/12, -sqrt(30)/12, -sqrt(10)/4
-3/4, sqrt(15)/12, sqrt(30)/12, sqrt(10)/4
-3/4, sqrt(15)/12, sqrt(30)/12, -sqrt(10)/4
Try these coordinates.
-3/4, -sqrt(15)/4, 0, 0
1/2, sqrt(15)/6, sqrt(30)/6, 0
1/2, -sqrt(15)/6, -sqrt(30)/6, 0
-1/2, sqrt(15)/6, sqrt(30)/6, 0
-1/2, -sqrt(15)/6, -sqrt(30)/6, 0
3/4, -sqrt(15)/12, sqrt(30)/6, 0
-3/4, sqrt(15)/12, -sqrt(30)/6, 0
1/2, sqrt(15)/6, -sqrt(30)/12, sqrt(10)/4
1/2, -sqrt(15)/6, sqrt(30)/12, sqrt(10)/4
1/2, sqrt(15)/6, -sqrt(30)/12, -sqrt(10)/4
1/2, -sqrt(15)/6, sqrt(30)/12, -sqrt(10)/4
-1/2, sqrt(15)/6, -sqrt(30)/12, sqrt(10)/4
-1/2, -sqrt(15)/6, sqrt(30)/12, sqrt(10)/4
-1/2, sqrt(15)/6, -sqrt(30)/12, -sqrt(10)/4
-1/2, -sqrt(15)/6, sqrt(30)/12, -sqrt(10)/4
3/4, -sqrt(15)/12, -sqrt(30)/12, sqrt(10)/4
3/4, -sqrt(15)/12, -sqrt(30)/12, -sqrt(10)/4
-3/4, sqrt(15)/12, sqrt(30)/12, sqrt(10)/4
-3/4, sqrt(15)/12, sqrt(30)/12, -sqrt(10)/4
Try these coordinates.
- Oschkar
- Mononian
- Posts: 15
- Joined: Fri Jul 03, 2009 5:49 pm
Re: Hypercube projection
Quickfur, you're back!
- Oschkar
- Mononian
- Posts: 15
- Joined: Fri Jul 03, 2009 5:49 pm
Re: Hypercube projection
Sorry for the late reply, apparently email notifications are broken so I didn't know you replied.
Anyway, are you sure these coordinates are right? I'm getting a 4D polytope with lots of (non-regular) octahedral facets. The orientation is a bit hard to discern cells in, I'll play around with it a bit to see if I can get a nice viewpoint.
Anyway, are you sure these coordinates are right? I'm getting a 4D polytope with lots of (non-regular) octahedral facets. The orientation is a bit hard to discern cells in, I'll play around with it a bit to see if I can get a nice viewpoint.
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Hypercube projection
Oh, and apparently some tetrahedral facets too. There are 30 facets in total, 20 distorted octahedra and 10 irregular tetrahedra.
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Hypercube projection
EDIT: actually, strike that. I graphed the vertex-connectivity of the tetrahedral cells, and found that they occur in two disjoint sets of 5 each, with every tetrahedron in each group sharing a vertex with every other tetrahedron (but no shared edges/faces).
The relationship of the octahedral cells with each other is much more complex, though. They appear to also be in two groups, this time of 10 each, with a decagrammic connectivity within each group, and complex connectivity between the groups.
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Hypercube projection
It's been almost a year, but I finally got to figuring out the entire coordinate system for this polytope.
1,0,0,0
-1/4,sqrt(15)/4,0,0
3/4,sqrt(15)/4,0,0
-1/4,-sqrt(15)/12,sqrt(30)/6,0
3/4,-sqrt(15)/12,sqrt(30)/6,0
-1/2,sqrt(15)/6,sqrt(30)/6,0
1/2,sqrt(15)/6,sqrt(30)/6,0
-1/4,-sqrt(15)/12,-sqrt(30)/12,sqrt(10)/4
3/4,-sqrt(15)/12,-sqrt(30)/12,sqrt(10)/4
-1/2,sqrt(15)/6,-sqrt(30)/12,sqrt(10)/4
1/2,sqrt(15)/6,-sqrt(30)/12,sqrt(10)/4
-1/2,-sqrt(15)/6,sqrt(30)/12,sqrt(10)/4
1/2,-sqrt(15)/6,sqrt(30)/12,sqrt(10)/4
-3/4,sqrt(15)/12,sqrt(30)/12,sqrt(10)/4
1/4,sqrt(15)/12,sqrt(30)/12,sqrt(10)/4
-1/4,-sqrt(15)/12,-sqrt(30)/12,-sqrt(10)/4
3/4,-sqrt(15)/12,-sqrt(30)/12,-sqrt(10)/4
-1/2,sqrt(15)/6,-sqrt(30)/12,-sqrt(10)/4
1/2,sqrt(15)/6,-sqrt(30)/12,-sqrt(10)/4
-1/2,-sqrt(15)/6,sqrt(30)/12,-sqrt(10)/4
1/2,-sqrt(15)/6,sqrt(30)/12,-sqrt(10)/4
-3/4,sqrt(15)/12,sqrt(30)/12,-sqrt(10)/4
1/4,sqrt(15)/12,sqrt(30)/12,-sqrt(10)/4
-1/2,-sqrt(15)/6,-sqrt(30)/6,0
1/2,-sqrt(15)/6,-sqrt(30)/6,0
-3/4,sqrt(15)/12,-sqrt(30)/6,0
1/4,sqrt(15)/12,-sqrt(30)/6,0
-3/4,-sqrt(15)/4,0,0
1/4,-sqrt(15)/4,0,0
-1,0,0,0
1,0,0,0
-1/4,sqrt(15)/4,0,0
3/4,sqrt(15)/4,0,0
-1/4,-sqrt(15)/12,sqrt(30)/6,0
3/4,-sqrt(15)/12,sqrt(30)/6,0
-1/2,sqrt(15)/6,sqrt(30)/6,0
1/2,sqrt(15)/6,sqrt(30)/6,0
-1/4,-sqrt(15)/12,-sqrt(30)/12,sqrt(10)/4
3/4,-sqrt(15)/12,-sqrt(30)/12,sqrt(10)/4
-1/2,sqrt(15)/6,-sqrt(30)/12,sqrt(10)/4
1/2,sqrt(15)/6,-sqrt(30)/12,sqrt(10)/4
-1/2,-sqrt(15)/6,sqrt(30)/12,sqrt(10)/4
1/2,-sqrt(15)/6,sqrt(30)/12,sqrt(10)/4
-3/4,sqrt(15)/12,sqrt(30)/12,sqrt(10)/4
1/4,sqrt(15)/12,sqrt(30)/12,sqrt(10)/4
-1/4,-sqrt(15)/12,-sqrt(30)/12,-sqrt(10)/4
3/4,-sqrt(15)/12,-sqrt(30)/12,-sqrt(10)/4
-1/2,sqrt(15)/6,-sqrt(30)/12,-sqrt(10)/4
1/2,sqrt(15)/6,-sqrt(30)/12,-sqrt(10)/4
-1/2,-sqrt(15)/6,sqrt(30)/12,-sqrt(10)/4
1/2,-sqrt(15)/6,sqrt(30)/12,-sqrt(10)/4
-3/4,sqrt(15)/12,sqrt(30)/12,-sqrt(10)/4
1/4,sqrt(15)/12,sqrt(30)/12,-sqrt(10)/4
-1/2,-sqrt(15)/6,-sqrt(30)/6,0
1/2,-sqrt(15)/6,-sqrt(30)/6,0
-3/4,sqrt(15)/12,-sqrt(30)/6,0
1/4,sqrt(15)/12,-sqrt(30)/6,0
-3/4,-sqrt(15)/4,0,0
1/4,-sqrt(15)/4,0,0
-1,0,0,0
- Oschkar
- Mononian
- Posts: 15
- Joined: Fri Jul 03, 2009 5:49 pm
Re: Hypercube projection
Thanks for the coordinates! Here's the very first render I did, from a viewpoint of <5,0,0,0>:
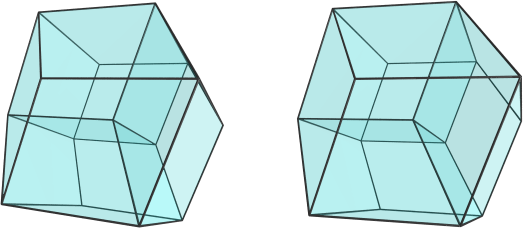
This looks awfully similar to the vertex-first projection of the tesseract, but actually, those hexahedral cells are not cubes, but parallelopipeds. Visibility clipping is on, so we can only see 4 cells, but actually, this shape has 20 cells. Here's a render with visibility culling turned off, and with edges on the far side of the shape rendered in blue so you can tell what's in front and what's behind:
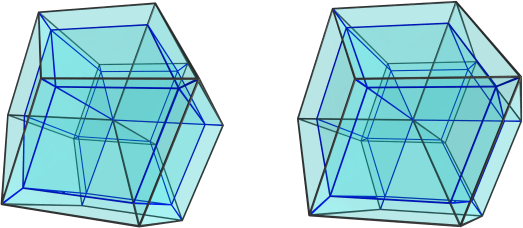
This image begins to show the structure of the shape. It appears to be made of 3 layers: the top and bottom layers are tetrahedral arrangements of parallelopiped cells, 4 each, and these two layers are connected to each other by a middle layer of 12 parallelopipeds. This particular viewpoint shows the "tesseract-within-a-tesseract" projection of the 5D cube, which is kinda cool.
Next, let's take a look from the side (<0,5,0,0>):
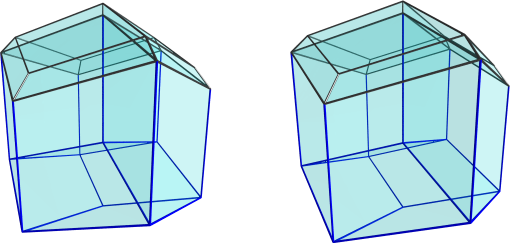
I've left the edges previously colored blue still colored blue, in order to give a point of reference as to where the 4D viewpoint is. The black edges on top of this image trace the outlines of the 4 parallelopipeds in the previous images. I've turned on visibility clipping again so that the image is not too cluttered; so only 3 of the previous 4 cells are visible here. Furthermore, they look flattened because we're looking at them from a 90° angle. They are not quite exactly 90° with the eye-to-object direction, so they don't appear completely flat, but they look quite flattened.
Below these cells are another 4 cells, also parallelopipeds. The bottom one is actually one of the cells from the bottom layer (the other 3 are not visible from this viewpoint because they lie behind this cell).
Next, let's turn off visibility clipping so that we can see the rest of the edges:

As you can see, it looks rather messy (which is why I usually like to leave visibility clipping on). But by comparing with the previous image, we can somewhat see which edges are on the far side of the shape from the current 4D viewpoint. If you look carefully, you can see 3 blue hexahedra at the bottom of the image, which share the bottom faces with the bottom cell from the previous image. These 4 cells are the cells in the bottom layer. The remaining middle-layer cells are really hard to see, because there are a lot of edges here, so let's do a sort of reverse-visclip, i.e., hide the cells on the near side of the shape from the current viewpoint, and show only those lying on the far side:
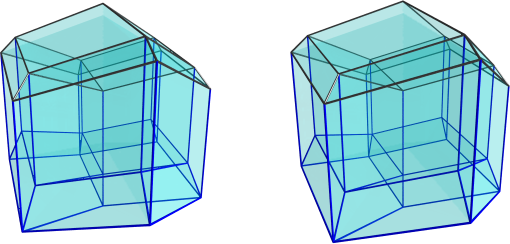
These are all the far-side cells. The bottom 3 cells on the far side are now much clearer. The middle layer cells are still a bit hard to see, but at least they are no longer overlapping each other's volumes, so if we look carefully, we can sorta tell where they are. If you look at the rhombus-shaped ridges at the top that has been foreshortened into narrow ridges, skirting around the top cell, you can see there are 6 of them in total, and below them are the squashed images of 6 parallelopiped cells. These 6 cells surround 3 cells at the center of the projection, which lie directly below the top cell. So that makes 9 cells in the middle layer, on the far side, which is 12 middle-layer cells in total.
Note that those 3 "inner" cells are actually the closest to the 4D viewpoint; the 6 squashed cells around the sides are being seen from a steep angle; they are near the limb of the projection image.
Finally, let's color the top and bottom layer cells so that it's easier to pick them out from the tangle of edges:
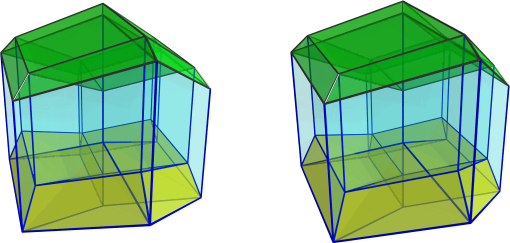
I've turned off visclip completely again, so that all cells are visible. Because there is no visclip, the cells overlap each other, but it shouldn't be too difficult to pick them out.
So in total, we have 4 top layer cells, 4 bottom layer cells, and 12 middle-layer cells. From the first and second images, you can see that these 12 middle-layer cells follow a rhombic-dodecahedral arrangement, so this projection of the 5D cube does show some kind of analogy to the rhombic dodecahedron. But it's not related to the 24-cell; instead, it has parallelopipeds for cells, with a combination of tetrahedral and rhombic dodecahedral arrangements. All in all, quite an interesting projection of the 5D cube, indeed!

This looks awfully similar to the vertex-first projection of the tesseract, but actually, those hexahedral cells are not cubes, but parallelopipeds. Visibility clipping is on, so we can only see 4 cells, but actually, this shape has 20 cells. Here's a render with visibility culling turned off, and with edges on the far side of the shape rendered in blue so you can tell what's in front and what's behind:

This image begins to show the structure of the shape. It appears to be made of 3 layers: the top and bottom layers are tetrahedral arrangements of parallelopiped cells, 4 each, and these two layers are connected to each other by a middle layer of 12 parallelopipeds. This particular viewpoint shows the "tesseract-within-a-tesseract" projection of the 5D cube, which is kinda cool.
Next, let's take a look from the side (<0,5,0,0>):
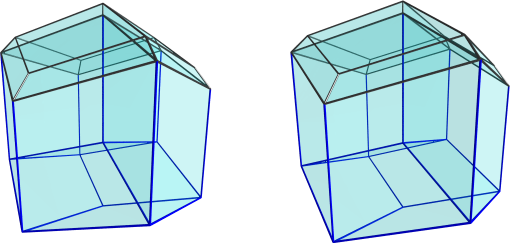
I've left the edges previously colored blue still colored blue, in order to give a point of reference as to where the 4D viewpoint is. The black edges on top of this image trace the outlines of the 4 parallelopipeds in the previous images. I've turned on visibility clipping again so that the image is not too cluttered; so only 3 of the previous 4 cells are visible here. Furthermore, they look flattened because we're looking at them from a 90° angle. They are not quite exactly 90° with the eye-to-object direction, so they don't appear completely flat, but they look quite flattened.
Below these cells are another 4 cells, also parallelopipeds. The bottom one is actually one of the cells from the bottom layer (the other 3 are not visible from this viewpoint because they lie behind this cell).
Next, let's turn off visibility clipping so that we can see the rest of the edges:

As you can see, it looks rather messy (which is why I usually like to leave visibility clipping on). But by comparing with the previous image, we can somewhat see which edges are on the far side of the shape from the current 4D viewpoint. If you look carefully, you can see 3 blue hexahedra at the bottom of the image, which share the bottom faces with the bottom cell from the previous image. These 4 cells are the cells in the bottom layer. The remaining middle-layer cells are really hard to see, because there are a lot of edges here, so let's do a sort of reverse-visclip, i.e., hide the cells on the near side of the shape from the current viewpoint, and show only those lying on the far side:

These are all the far-side cells. The bottom 3 cells on the far side are now much clearer. The middle layer cells are still a bit hard to see, but at least they are no longer overlapping each other's volumes, so if we look carefully, we can sorta tell where they are. If you look at the rhombus-shaped ridges at the top that has been foreshortened into narrow ridges, skirting around the top cell, you can see there are 6 of them in total, and below them are the squashed images of 6 parallelopiped cells. These 6 cells surround 3 cells at the center of the projection, which lie directly below the top cell. So that makes 9 cells in the middle layer, on the far side, which is 12 middle-layer cells in total.
Note that those 3 "inner" cells are actually the closest to the 4D viewpoint; the 6 squashed cells around the sides are being seen from a steep angle; they are near the limb of the projection image.
Finally, let's color the top and bottom layer cells so that it's easier to pick them out from the tangle of edges:

I've turned off visclip completely again, so that all cells are visible. Because there is no visclip, the cells overlap each other, but it shouldn't be too difficult to pick them out.
So in total, we have 4 top layer cells, 4 bottom layer cells, and 12 middle-layer cells. From the first and second images, you can see that these 12 middle-layer cells follow a rhombic-dodecahedral arrangement, so this projection of the 5D cube does show some kind of analogy to the rhombic dodecahedron. But it's not related to the 24-cell; instead, it has parallelopipeds for cells, with a combination of tetrahedral and rhombic dodecahedral arrangements. All in all, quite an interesting projection of the 5D cube, indeed!
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Hypercube projection
It looks even more intriguing than I thought it would! It seems that all my suspicions about this shape were confirmed:
1. It has 20 parallelepiped cells.
2. The 4 cells at the top are arranged in the opposite fashion to 4 on the bottom.
3. If you merge the cells into rhombic dodecahedra you end up with a pentatope.
4. The rhombic icosachoron can be projected to show one rhombic dodecahedron inside another.
1. It has 20 parallelepiped cells.
2. The 4 cells at the top are arranged in the opposite fashion to 4 on the bottom.
3. If you merge the cells into rhombic dodecahedra you end up with a pentatope.
4. The rhombic icosachoron can be projected to show one rhombic dodecahedron inside another.
Last edited by Oschkar on Fri Feb 22, 2013 2:30 pm, edited 1 time in total.
- Oschkar
- Mononian
- Posts: 15
- Joined: Fri Jul 03, 2009 5:49 pm
Re: Hypercube projection
This figure is in the polygloss as a strombiated simplex. This means that its faces are all anti-tegums of the margins of the simplex.
The volume of a strombiated simplex, in N dimensions, is sqrt(N+1), where the in-diameter is sqrt(2). Since this figure is the venori cell of the A_n tiling (ie the 60-degree rombus), the packing efficiency of this tiling is 1/sqrt(N+1). It is the most efficient packing in 2d and 3d, but there are more efficient ways of packing spheres in 4d and higher. So much so, that by seven dimensions, one can place a full second copy of it in the same space, (3_31) and in eight dimensions, three (5_21).
Not only does the strombiated simplex tile space, but there is a tiling comprising of the N+1 squashed measure-polytopes, in the manner of the 'cats eye' in 2d, etc. That is, it is possible to place such squashed parallelotopes such that the axis of shrinkings meet at specific corners.
The general vertices in N dimensions can be thus determined.
1. The vertices consist of all N+1 combinations of 0 and 1, except for all 0's and all 1's (ie the axis of projection).
2. One needs to reduce this N+1 points so that the sum is zero. This is done by subtracting some x from each coordinate.
3. The points thus constructed then fall on the plane x+y+z... = 0, in the projection of the line x=y=z=...
So here we have, eg (with all permutations).
1,1,1,1,0 becomes 0.2, 0.2, 0.2, 0.2, -0.8
1,1,1,0,0 becomes 0.4, 0.4, 0.4, -0.6, 0.6
1,1,0,0,0 becomes 0.6, 0.6, -0.4, -0.4, -0.4
1,0,0,0,0 becomes 0.8, -0.2, -0.2, -0.2, -0.2
Once one constructs a set of coordinates for this thing, eg
r5, r5, r5, -1
-r5, -r5, r5, -1
-r5, r5, -r5, -1
r5, -r5, -r5, -1
0, 0, 0, 4
One then adds up the five coordinates, like 1,1,1,1,0 etc over these five axies, to get the 30 vertices of this figure. It really doesn't matter whether you use the reduced set or the unreduced set, since the vector 1,1,1,1,1 is the same as 0,0,0,0,0 anyway.
So that's how you find the coordinates of these things.
The volume of a strombiated simplex, in N dimensions, is sqrt(N+1), where the in-diameter is sqrt(2). Since this figure is the venori cell of the A_n tiling (ie the 60-degree rombus), the packing efficiency of this tiling is 1/sqrt(N+1). It is the most efficient packing in 2d and 3d, but there are more efficient ways of packing spheres in 4d and higher. So much so, that by seven dimensions, one can place a full second copy of it in the same space, (3_31) and in eight dimensions, three (5_21).
Not only does the strombiated simplex tile space, but there is a tiling comprising of the N+1 squashed measure-polytopes, in the manner of the 'cats eye' in 2d, etc. That is, it is possible to place such squashed parallelotopes such that the axis of shrinkings meet at specific corners.
The general vertices in N dimensions can be thus determined.
1. The vertices consist of all N+1 combinations of 0 and 1, except for all 0's and all 1's (ie the axis of projection).
2. One needs to reduce this N+1 points so that the sum is zero. This is done by subtracting some x from each coordinate.
3. The points thus constructed then fall on the plane x+y+z... = 0, in the projection of the line x=y=z=...
So here we have, eg (with all permutations).
1,1,1,1,0 becomes 0.2, 0.2, 0.2, 0.2, -0.8
1,1,1,0,0 becomes 0.4, 0.4, 0.4, -0.6, 0.6
1,1,0,0,0 becomes 0.6, 0.6, -0.4, -0.4, -0.4
1,0,0,0,0 becomes 0.8, -0.2, -0.2, -0.2, -0.2
Once one constructs a set of coordinates for this thing, eg
r5, r5, r5, -1
-r5, -r5, r5, -1
-r5, r5, -r5, -1
r5, -r5, -r5, -1
0, 0, 0, 4
One then adds up the five coordinates, like 1,1,1,1,0 etc over these five axies, to get the 30 vertices of this figure. It really doesn't matter whether you use the reduced set or the unreduced set, since the vector 1,1,1,1,1 is the same as 0,0,0,0,0 anyway.
So that's how you find the coordinates of these things.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2014
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Hypercube projection
Can you show it from (5sqrt2/2,5sqrt2/2,0,0)? I'd like to see what a middle view might look like.
- Oschkar
- Mononian
- Posts: 15
- Joined: Fri Jul 03, 2009 5:49 pm
Re: Hypercube projection
Oschkar wrote:Can you show it from (5sqrt2/2,5sqrt2/2,0,0)? I'd like to see what a middle view might look like.
Hi, sooo sorry for the extremely late response. As I said in the other thread, I've been too busy with other things. Anyway, here's a render from your given viewpoint:
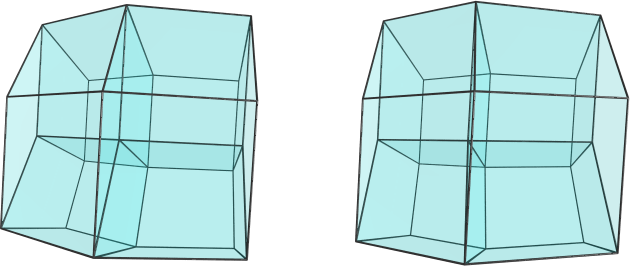
Seems like just the usual rhombic dodecahedral projection. There are 6 parallelopiped cells visible here. The vertex in the center is the closest to the 4D viewpoint (as usual for a convex shape).
Well, visclip is on, so let's see what's hiding behind these near-side cells:
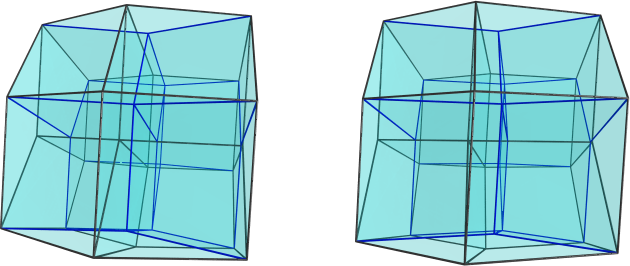
The blue lines are edges that lie on the far side of the polytope. There seems to be an axis of symmetry of some sort horizontally across the middle of the image, so let's re-orient the polytope a bit to get another look at it (well actually, I just played around with the povray 3D viewpoint, so no change in the 4D viewpoint here):
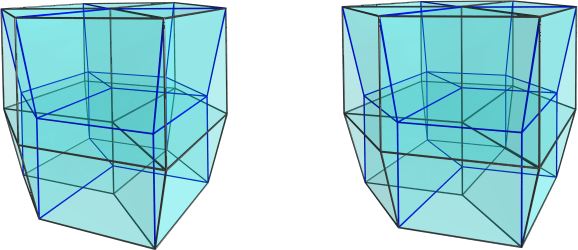
From this view, looks like we have 6 hexahedral cells on the near side, 6 hexahedral cells on the far side, joined by a ring of 6 hexahedral cells that circle around the sides. Two more cells appear at the top and bottom (the top one is a bit hard to see from this angle, it's almost flattened into a hexagon). So that's 20 cells in total, which accounts for all of them.
If you have any suggestions about how to do further renders, just let me know. I wasn't quite sure what you were looking for, so these are just generic first-try attempts. If you want some cells highlighted, etc., I can try to do that as well; that might help locate some of the more obscure parts (although I think this particular viewpoint is pretty good, all of the cells can be picked out without too much difficulty).
Well, hope this helps! (And sorry again for the late response!)
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
16 posts
• Page 1 of 1
Who is online
Users browsing this forum: No registered users and 38 guests
