Secret wrote:ICN5D
Love those gifs
Thanks! Super cool, aren't they? Nothing better than live action footage of what we've been talking about.
Now I can double check my visualisation progress and see if there are errors in my drawings
Let me know if you want to see something specific, that I haven't made already. I'll totally make one on special request, for anyone. I'm hoping that the GIFs will stir up some more interest, and get others to ask questions. It's mostly been Marek and myself going back and forth, developing on new ideas. A really good one was the " Inflation Sequence " of ' A along B ' method of reducing them. We developed it based on Polyhedron Dude's naming system of 'small shape along large shape'. Come to find out, it's
extremely useful for a visual aid, and the way it matches up in toratope notation is paramount to one's comprehension. We can now describe +10D toratopes very easily with this reduction.
I am miles behind this thread now due to uni and stuff, it might took a while to catch up and start makings cuts with you guys
I know, right? It evolved so very quickly. Well, again, feel free to ask about previous stuff. There's valuable insights scattered randomly all throughout this thread. It's tough to pick out the noteworthy ones, in the midst of everything else. I'm just an accomplished apprentice, Marek will always be the Zen Toratope Master

Marek wrote:Hmm, would this make it easier to derive cages for more than four points?
I'm thinking so. Ultimately, any and all margins come from the implicit surface equation, we just remove the final minor diameter to deflate it. In the way I see it, if tiger is :
((II)(II)) -- (sqrt(x^2 + y^2) - R1a)^2 + (sqrt(z^2 + w^2) - R1b)^2 - R2^2 = 0
then a duoring would be :
(sqrt(x^2 + y^2) - R1a)^2 + (sqrt(z^2 + w^2) - R1b)^2 = 0
and we can use :
(sqrt(x^2 + (y*sqrt(2)/2 + w*sqrt(2)/2)^2) - R1a)^2 + (sqrt(z^2 + (y*sqrt(2)/2 - w*sqrt(2)/2)^2) - R1b)^2 = 0
to rotate 45 degrees, then cut to 3D:
(sqrt(x^2 + (y*sqrt(2)/2 + a*sqrt(2)/2)^2) - R1a)^2 + (sqrt(z^2 + (y*sqrt(2)/2 - a*sqrt(2)/2)^2) - R1b)^2 = 0
where when a=0 , we have the infinitely thin tiger cage. The minor diameter R2 needs some value to flesh it out in CalcPlot, at least 0.25 with 40 cube rendering.
So, then for a duoring torus, the edge of a cyltorinder, we use the function from (((II)I)(II)) :
(sqrt((sqrt(x^2 + y^2) - R1)^2 + z^2) - R2a)^2 + (sqrt(w^2 + v^2) - R2b)^2 - R3^2 = 0
deflate R3 to make just the edge of a ((II)I)(II) , tracing out to 8 points in a 4x2 array:
(sqrt((sqrt(x^2 + y^2) - R1)^2 + z^2) - R2a)^2 + (sqrt(w^2 + v^2) - R2b)^2 = 0
From this, we'll have to reconcile the property of the single major diameter, and the two equal mediums for a proper cage. The mediums R2a and R2b will be identical to the tiger cage rewriting, but I'm not sure how to add in the major R1. When it happens, we get close to the hexatangent cut of (((II)I)(II)), which has a tangent cluster that can inscribe an octahedron

I'll have to play with the sliders, and get some values to reverse derive a technique. A good place to start may be:
(sqrt((sqrt(x^2 + y^2) - R1)^2 + (z*sqrt(2)/2 + v*sqrt(2)/2)^2) - R2a)^2 + (sqrt(w^2 + (z*sqrt(2)/2 - v*sqrt(2)/2)^2) - R2b)^2 = 0
From here, I suppose a rotation around XW or YW would be worthy to consider. Like, maybe:
(sqrt((sqrt(x^2 + (y*sqrt(2)/2 + w*sqrt(2)/2)^2) - R1)^2 + (z*sqrt(2)/2 + v*sqrt(2)/2)^2) - R2a)^2 + (sqrt((y*sqrt(2)/2 - w*sqrt(2)/2)^2 + (z*sqrt(2)/2 - v*sqrt(2)/2)^2) - R2b)^2 = 0
???
One can do this with the quad tiger cage from (((II)I)((II)I)), as it's two identical duorings, a smaller inflating a larger:
(sqrt((sqrt(x^2 + y^2) - R1a)^2 + z^2) -R2a)^2 + (sqrt((sqrt(w^2 + v^2) - R1b)^2 + u^2) - R2b)^2 - R3^2 = 0
and R3 deflates to :
(sqrt((sqrt(x^2 + y^2) - R1a)^2 + z^2) -R2a)^2 + (sqrt((sqrt(w^2 + v^2) - R1b)^2 + u^2) - R2b)^2 = 0
then we rewrite to :
(sqrt((sqrt(x^2 + (y*sqrt(2)/2 + v*sqrt(2)/2)^2) - R1a)^2 + (z*sqrt(2)/2 + u*sqrt(2)/2)^2) -R2a)^2 + (sqrt((sqrt(w^2 + (y*sqrt(2)/2 - v*sqrt(2)/2)^2) - R1b)^2 + (z*sqrt(2)/2 - u*sqrt(2)/2)^2) - R2b)^2 = 0
for a true 45x45 degree slice of a di-duoring, duoring inflated duoring. But, since this structure is a multiplication of the surface of two torii, which have a big+small circle, we get a binomial expansion into big+big , big+small , small+big , and small+small . Which cuts at 45 degrees to make only two tiger cages of big+big and small+small .
This inspires me to make a showcase of just the polyrings themselves. I already have a few pics and GIFs made just for it, too. It'll be good to discuss the edges of the open toratope prisms, as all closed toratopes are nothing more than an inflated edge. I should probably make another thread on opens as well, with their surtopes and enumeration algorithm.
Which brings me back to a previous post, about the open toratope implicit equations:
Implicit equation for open toratopes are easy -- you just don't use all coordinates. For example, x^2 + y^2 = 1 is equation of circle in 2D, but equation of infinite cylinder in 3D and equation of circle x plane in 4D.
How can I close up the ends on a cylinder, in the 3D rendering program? I might want to make slice animations of a cubinder, or cyltorinder ( duocylinder torus ). Also, what would the equation for a cyltrianglinder be? It has three cylinders joined by a triangle torus in a triangular configuration. In my notation it'll be :
[ I>IO • {3^IOI + I>(O)} • {3:IO + 3^I(O)} • 3:(O) •-• n ]
which I'm inclined to develop a way to convert it into implicits. That'll be the next big step!
It's really close to the oblique cut (((O)I)((O)I)) , between (((I)I)(()I)) and ((()I)((I)I)). The two tiger cages oblique. I've got an animation coming of that one, too! I rotated to 45 degrees between the square of four tigers (((I)I)((I)I)) , and translated out. Moving past the square at a 45 degree angle is super cool to see a 1x2x1 oblique evolution of the four tigers, cutting the square like a diamond. Again, that new function is absolutely amazing. One can actually pilot a 3D hyperplane around this way, without being tethered to the origin. Like steering an extra-dimensional spaceship, it's way cool going out to survey geometric structures in their home dimension
Just wait, I'm cooking up some insane animation ideas .....
 I'm glad I could help
I'm glad I could help 

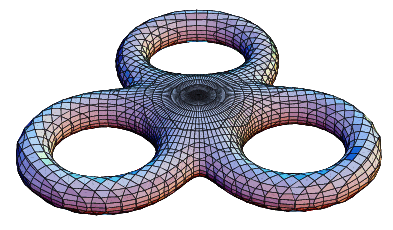
 . That took a little bit of time in itself, just to enumerate them and delete duplicates! I've been trying to break them down by diameter hierarchy lately, using the inflation process as a reference. So, apparently, ((((II)I)(II))(II)(II)) has one major, two equal secondaries, one tertiary, two equal quaternaries, and a minor diameter. Keeping all of the empty cuts makes the combinatorics more clear. Next step is a description of the cuts ....
. That took a little bit of time in itself, just to enumerate them and delete duplicates! I've been trying to break them down by diameter hierarchy lately, using the inflation process as a reference. So, apparently, ((((II)I)(II))(II)(II)) has one major, two equal secondaries, one tertiary, two equal quaternaries, and a minor diameter. Keeping all of the empty cuts makes the combinatorics more clear. Next step is a description of the cuts ....  I'll have to play with the sliders, and get some values to reverse derive a technique. A good place to start may be:
I'll have to play with the sliders, and get some values to reverse derive a technique. A good place to start may be: