The Tiger Explained
I don't even know what you're claiming anymore. Are you saying they're topologically equivalent, or exactly the same object (up to a change of parameters or a rotation)?
Note that the 3-torus has a major radius, a middle radius and a minor radius, while the tiger has two minor radii and a major radius. If the objects are the same, you need a transformation that takes the three radii of the tiger, and returns the three radii of the equivalent 3-torus. If you can visualise the objects as easily as you claim, it shouldn't be hard to find this transformation.
Note that the 3-torus has a major radius, a middle radius and a minor radius, while the tiger has two minor radii and a major radius. If the objects are the same, you need a transformation that takes the three radii of the tiger, and returns the three radii of the equivalent 3-torus. If you can visualise the objects as easily as you claim, it shouldn't be hard to find this transformation.
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
As the inventor of the name "tiger", I feel obliged to add something.
One way to generate tiger naturally, together with other toratopes in 4D, is simply to consider rotations.
If we start with a circle in 2D, there are two different ways to rotate it: either around a bisecting line, or around a non-intersecting line. First way results in a sphere, second in torus.
Now, there are, similarly, two ways to rotate a sphere. If we rotate it around a bisecting plane, we get a glome. But if we rotate it around a non-intersecting plane, we get (211).
There are, then, FOUR ways to rotate a torus, since it has two distinct kinds of coordinate planes.
If we put torus's main circle in xy plane, then rotation around xy plane (and parallel) is different than rotation around xz or yz. Thus, we can produce four different shapes by rotating a torus:
xy, bisecting: (211)
xy, non-intersecting: (22) - TIGER
xz, bisecting: (31)
xz, non-intersecting: ((21)1) - tetratorus
The general rule for rotating a toratope is like this:
1. Reduce it to unary notation (all ones). Tiger would be ((11)(11)).
2. You rotate around a coordinate hyperplane (or a parallel plane). It has all the dimensions (ones) of the figure - except for one. Replace that one with X. In our case, we can replace any of the four, and get an equivalent representation:
((X1)(11))
3. If you rotated around a BISECTING plane, replace X with 11. If you rotated around a NON-INTERSECTING PLANE, replace X with (11)
((111)(11)) - bisecting
(((11)1)(11)) - non-intersecting
4. Collapse it back
(32) - bisecting
((21)2) - non-intersecting
One way to generate tiger naturally, together with other toratopes in 4D, is simply to consider rotations.
If we start with a circle in 2D, there are two different ways to rotate it: either around a bisecting line, or around a non-intersecting line. First way results in a sphere, second in torus.
Now, there are, similarly, two ways to rotate a sphere. If we rotate it around a bisecting plane, we get a glome. But if we rotate it around a non-intersecting plane, we get (211).
There are, then, FOUR ways to rotate a torus, since it has two distinct kinds of coordinate planes.
If we put torus's main circle in xy plane, then rotation around xy plane (and parallel) is different than rotation around xz or yz. Thus, we can produce four different shapes by rotating a torus:
xy, bisecting: (211)
xy, non-intersecting: (22) - TIGER
xz, bisecting: (31)
xz, non-intersecting: ((21)1) - tetratorus
The general rule for rotating a toratope is like this:
1. Reduce it to unary notation (all ones). Tiger would be ((11)(11)).
2. You rotate around a coordinate hyperplane (or a parallel plane). It has all the dimensions (ones) of the figure - except for one. Replace that one with X. In our case, we can replace any of the four, and get an equivalent representation:
((X1)(11))
3. If you rotated around a BISECTING plane, replace X with 11. If you rotated around a NON-INTERSECTING PLANE, replace X with (11)
((111)(11)) - bisecting
(((11)1)(11)) - non-intersecting
4. Collapse it back
(32) - bisecting
((21)2) - non-intersecting
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
3. If you rotated around a BISECTING plane, replace X with 11. If you rotated around a NON-INTERSECTING PLANE, replace X with (11)
That's a nice construction. I think it's related to the way I derived the formula for the rotopes.
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
PWrong writes
In a normal torus, we have an undistorted circle in yz, and a second circle written in the axis rx (say). This produces a mapping of the 4d plane wx into a distortion in rx, and r becomes the axis of pondering.
The 3-torus only has these different radii because of the way the pondering axies are set. If the axies are colinear, then indeed you will get nested distortion.
We should visualise the torus in 3d, to see what is happening. If we simply spherate the surface (in 4d), we produce a figure that does indeed have axies of 3 types. But the torus product is not a matter of spheration. It merges two spaces (and figures inscribed in each), such that the two spaces cross in a line, and one of the figures is centred on the surface of the other, and distorted in the direction of the line.
So for the torus, the actual process of spheration replaces a point by a circle centred on that point, the new circle lies in the direction of the radius and the w axis.
On the other hand, if the direction of forshortning is in the direction of the axle of the torus (ie the line where the axle would fall), then the forshortning would not disturb the symmetry of yz, the result would create perfect spherical symmetry in yz.
One should always remember that a duocylinder can be rendered from circles of any size, one is not obliged to stick with equal size circles.
W
Note that the 3-torus has a major radius, a middle radius and a minor radius, while the tiger has two minor radii and a major radius. If the objects are the same, you need a transformation that takes the three radii of the tiger, and returns the three radii of the equivalent 3-torus. If you can visualise the objects as easily as you claim, it shouldn't be hard to find this transformation.
In a normal torus, we have an undistorted circle in yz, and a second circle written in the axis rx (say). This produces a mapping of the 4d plane wx into a distortion in rx, and r becomes the axis of pondering.
The 3-torus only has these different radii because of the way the pondering axies are set. If the axies are colinear, then indeed you will get nested distortion.
We should visualise the torus in 3d, to see what is happening. If we simply spherate the surface (in 4d), we produce a figure that does indeed have axies of 3 types. But the torus product is not a matter of spheration. It merges two spaces (and figures inscribed in each), such that the two spaces cross in a line, and one of the figures is centred on the surface of the other, and distorted in the direction of the line.
So for the torus, the actual process of spheration replaces a point by a circle centred on that point, the new circle lies in the direction of the radius and the w axis.
On the other hand, if the direction of forshortning is in the direction of the axle of the torus (ie the line where the axle would fall), then the forshortning would not disturb the symmetry of yz, the result would create perfect spherical symmetry in yz.
One should always remember that a duocylinder can be rendered from circles of any size, one is not obliged to stick with equal size circles.
W
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
But the torus product is not a matter of spheration. It merges two spaces (and figures inscribed in each), such that the two spaces cross in a line, and one of the figures is centred on the surface of the other, and distorted in the direction of the line.
The torus product is spheration. They both have the same definition. They don't have anything to do with spaces crossing in a line.
As for the rest of your post, I still don't follow you.
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
The torus product runs like this.
Suppose you take a polytope P. You can replace the p surtopes of P with a little prism pQ, and fit the whole thing together as a torus.
For example, consider the hexagon. If you replace the edges of the hexagon with a pentagonal bar, and line these up so that the pentagons link up, you get something like a pentagonal column that has been bent into the shape of a hexagon.
In four dimensions, you can do the same thing with a dodecahedral column. Bend it into the shape of a polygon, and you get a dodecahedral - polygon torus.
Note there is some distortion as you do the bending: the inner side is shorter than the outside.
The 'tetratorus' and the 'tiger' are both formed from a bar whose cross section is a 3d torus. The main difference is that when we bend this bar into a circle, we impose an axis of compression (pondering) on the torus, so that the circles on the inside are shorter than those on the outside.
This axis runs like an axle in the tiger, and like a spoke on the tetratorus.
It should also be recalled that spheration is itself not a product, but a transformation. That is, the spheration is not of the form A × B, but more of the form f(A). The torus product is a product of two free figures (ie there is no restriction on A and B). Spheration merely corresponds to B = line ø^ n [sphere-power].
The point is that one can replace the sphere of spheation by the orthogonals to the sphere (eg circles), and then draw in that circle a polytope.
One can, in like manner, start with a figure, and replace its faces with prisms such that the bases of the prisms match the next base. For example, one can fold a column of prisms, with some distortion, into a ring, this ring being made of prisma (offcuts of a column), which corresponds in total to the cartesian product of the surfaces.
In fact, the value of the torus product is that it can be applied freely to surfaces to get a product, in the same way that the prism product can apply to solids.
Suppose you take a polytope P. You can replace the p surtopes of P with a little prism pQ, and fit the whole thing together as a torus.
For example, consider the hexagon. If you replace the edges of the hexagon with a pentagonal bar, and line these up so that the pentagons link up, you get something like a pentagonal column that has been bent into the shape of a hexagon.
In four dimensions, you can do the same thing with a dodecahedral column. Bend it into the shape of a polygon, and you get a dodecahedral - polygon torus.
Note there is some distortion as you do the bending: the inner side is shorter than the outside.
The 'tetratorus' and the 'tiger' are both formed from a bar whose cross section is a 3d torus. The main difference is that when we bend this bar into a circle, we impose an axis of compression (pondering) on the torus, so that the circles on the inside are shorter than those on the outside.
This axis runs like an axle in the tiger, and like a spoke on the tetratorus.
It should also be recalled that spheration is itself not a product, but a transformation. That is, the spheration is not of the form A × B, but more of the form f(A). The torus product is a product of two free figures (ie there is no restriction on A and B). Spheration merely corresponds to B = line ø^ n [sphere-power].
The point is that one can replace the sphere of spheation by the orthogonals to the sphere (eg circles), and then draw in that circle a polytope.
One can, in like manner, start with a figure, and replace its faces with prisms such that the bases of the prisms match the next base. For example, one can fold a column of prisms, with some distortion, into a ring, this ring being made of prisma (offcuts of a column), which corresponds in total to the cartesian product of the surfaces.
In fact, the value of the torus product is that it can be applied freely to surfaces to get a product, in the same way that the prism product can apply to solids.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Suppose you take a polytope P. You can replace the p surtopes of P with a little prism pQ, and fit the whole thing together as a torus.
Not in any unique way. You can change the angle of pQ however you like, and the result will still be a torus product of your two shapes. Your definition of the torus product is multi-valued. That is, it would be if you had a definition.
The 'tetratorus' and the 'tiger' are both formed from a bar whose cross section is a 3d torus.
Are you talking about the torinder (torus x line)? Why don't you just call it that?
The main difference is that when we bend this bar into a circle, we impose an axis of compression (pondering) on the torus, so that the circles on the inside are shorter than those on the outside.
You haven't defined "bend", and I can't think of any acceptable definition for it. It's not a linear map, but it's not as general as a continuous map.
Give me a unique equation, or even a good unique description, for something like circle#square or helix#triangle, and I'll agree that the torus product is defined for any two shapes.
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
Not in any unique way. You can change the angle of pQ however you like, and the result will still be a torus product of your two shapes. Your definition of the torus product is multi-valued. That is, it would be if you had a definition.
Like the prism product, the tegum product, the pyramid product, and the spheration product, the torus product has additional parameters. That is, there is more to A×B than is inherent in A and B itself. Prism products, for example, can be oblique. One gets an egg shape by making one of the two lines cross off-centre, and spherating it, and the kite is little more than an off-centre tegum-product.
In the case of the torus product, it is possible to set an axis of pondering, and a scale for that axis.
The fact is that you can't do the torus product in a unique way, even with spheres, because the product is pondering, or dimension-loosing.
Are you talking about the torinder (torus x line)? Why don't you just call it that?
Why not just call it the tri-circular torus. That's what it is.
Are you talking about the torinder (torus x line)? Why don't you just call it that?
helix × triangle is not possible, because the product is a surface product. You can only do general shapes if the product is solid.
A circle × square is a 3d figure. You can get the shape, for example, from the circle at x²+y² = r² = R². You can render it into a square by placing eg
x²+y² = r², abs(r-n)+abs(z) < E/sqrt(2).
x²+y² = r², max (r-n, z) < E/2
The first gives a circular ring of diamond-shape section. The second gives a shape not dis-similar to a square X-section washer.
You should further understand that spheration does not in itself lead to figures with holes in it. Spheration does not create holes. On the other hand, the torus product can't but create holes.
Spheration was originally invented to describe the sort of ball and pipe structures that ray-tracing is apt to produce. However, even here, one can fill in the faces, so a suitably ray-traced dodecahedron might be described as spherated even though it has no holes.
What spheration does do is to render elsewise flat surtopes into solids. A point is inaccessable, but a sphere is something you can grab and make models from.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Like the prism product, the tegum product, the pyramid product, and the spheration product, the torus product has additional parameters.
Well, you should include these parameters in your definition. It's still multi-valued though. Actually, I don't think you can describe it with a finite number of parameters (see below).
Why not just call it the tri-circular torus. That's what it is.
how do you get tri-circular torus from (circle#circle)xline?
helix × triangle is not possible, because the product is a surface product. You can only do general shapes if the product is solid.
What do you mean by solid? Helix # circle is possible, as is any smooth curve # circle.
For circle # square, you give two possible shapes. But there are infinitely many in between these. You could express them with an angle, theta for where the axis is. But theta doesn't have to be constant. What if you start with a square cross-section, then rotate the square as you go around the circle? When you get to the other side it would be a diamond, then when you get back to the start it's a square again. So your additional parameter can be any function of the parameter of the circle. This gets extremely ambiguous when you're talking about complicated objects like helixes.
Btw, you should distinguish between x and #. They are both special cases of the true cartesian product. But the cartesian product depends on the position and orientation of the two objects.
For instance, circle x circle = duocylinder, circle # circle = torus, but the cartesian product of two circles depends on where the circles are.
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
PWrong wrote:For instance, circle x circle = duocylinder, circle # circle = torus, but the cartesian product of two circles depends on where the circles are.
circle # circle = torus. do you mean like this
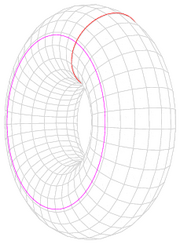
circle x circle = duocylinder. so for every point in circle 1 there exists all points in circle 2. and for every point in circle 2 there exists all points in circle 1? to make a duocylinder do you need to define the dimension the cicles occupy in relation to each other? or does it work without the specification?
or did I not follow corectly?
too many people have self replicating sigs. Don't copy this.
- batmanmg
- Trionian
- Posts: 201
- Joined: Sun Aug 20, 2006 10:21 pm
Why should a product be defined in terms of a finite number of parameters? I don't understand.
Firstly, it is not exactly clear how the enclosing spaces ought be positioned, if all we have is a single point of crossing? For example, consider the way that two eight-dimensional spaces cross in 16 dimensions?
Secondly, many of the products have centres of product. The torus product has also pondering axies.
Do we need all of these parameters? If you want to specifically qualify a specific object then yes. But the general utility of these products do not need such a thing. One might for example, consider the definition of parameters to define unique pentatopes (which are, after all, the fifth power of the point under pyramid product).
These are not even cartesian products! In the Euclidean space, they overlap with the cartesian product, but the current symbols for these products are ## and #* (for prism and comb products). One notes that the cartesian product does not encompass all products, because ** pyramid products and *# tegum product are not cartesian under any stretch of the imagination. Nor is the general () spheration.
In any case, provision is made to provide indexure (power series) on any of these, by using a symbol @, where the index goes on the @ side, and the root goes on the sign side, eg cube = line #*@ 3.
The four properties #*, *#, ##, and ** have properties based on whether the first/second sign is #/*, eg
So the *# tegum product is the draft of the surface, which for both losing and gaining a dimension, remains the same.
The prism product #* is an extension of the content, that is, each point of the content is replaced by a copy of the content of the second element.
The comb product ## is an extension of the surface: there is only a copy of the surface for each point of the surface of the original. The body is created anew.
The pyramid product ** draws the content, and therefore adds a dimension by the process.
The dual of a product, is the dual-product (by reversal of the symbols), of the dual, eg dual of the product X, #* Y is X' *# Y'.
The "cartesian product" is #-. It has no meaning outside Euclidean geometry.
The torus product is ##, along with the other comb products (eg the "cartesian product" of tilings.
Note that one can regard tilings as "covering" a solid space behind it, and do comb products. This gives, eg
One notices here that the topological equals of the torus is of the corresponding lattice. That is, the {5}##{6} comb is a portion of the {oo}##{oo} comb, and not the {5}#*{6} prism: there are no pentagons or hexagons.
Firstly, it is not exactly clear how the enclosing spaces ought be positioned, if all we have is a single point of crossing? For example, consider the way that two eight-dimensional spaces cross in 16 dimensions?
Secondly, many of the products have centres of product. The torus product has also pondering axies.
Do we need all of these parameters? If you want to specifically qualify a specific object then yes. But the general utility of these products do not need such a thing. One might for example, consider the definition of parameters to define unique pentatopes (which are, after all, the fifth power of the point under pyramid product).
Btw, you should distinguish between x and #. They are both special cases of the true cartesian product. But the cartesian product depends on the position and orientation of the two objects.
These are not even cartesian products! In the Euclidean space, they overlap with the cartesian product, but the current symbols for these products are ## and #* (for prism and comb products). One notes that the cartesian product does not encompass all products, because ** pyramid products and *# tegum product are not cartesian under any stretch of the imagination. Nor is the general () spheration.
In any case, provision is made to provide indexure (power series) on any of these, by using a symbol @, where the index goes on the @ side, and the root goes on the sign side, eg cube = line #*@ 3.
The four properties #*, *#, ##, and ** have properties based on whether the first/second sign is #/*, eg
- Code: Select all
#_ The product is extensive
*_ The product draws (adds a dimension)
_# The surface is mulitopied (product ponders = loses a dimension)
_* The content is multiplied
So the *# tegum product is the draft of the surface, which for both losing and gaining a dimension, remains the same.
The prism product #* is an extension of the content, that is, each point of the content is replaced by a copy of the content of the second element.
The comb product ## is an extension of the surface: there is only a copy of the surface for each point of the surface of the original. The body is created anew.
The pyramid product ** draws the content, and therefore adds a dimension by the process.
The dual of a product, is the dual-product (by reversal of the symbols), of the dual, eg dual of the product X, #* Y is X' *# Y'.
The "cartesian product" is #-. It has no meaning outside Euclidean geometry.
The torus product is ##, along with the other comb products (eg the "cartesian product" of tilings.
- Code: Select all
circle ## circle = torus (3d)
circle #* circle = bi-circular tegum (4d)
circle *# circle = bi-circular prism (4d)
circle ** circle = bi-circular pyramid (5d)
Note that one can regard tilings as "covering" a solid space behind it, and do comb products. This gives, eg
- Code: Select all
apeirogon ## apeirogon = square lattice (2t = 3d)
apeirogon ## square lat = cubic lattice (3t = 4d)
One notices here that the topological equals of the torus is of the corresponding lattice. That is, the {5}##{6} comb is a portion of the {oo}##{oo} comb, and not the {5}#*{6} prism: there are no pentagons or hexagons.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Why should a product be defined in terms of a finite number of parameters? I don't understand.
When you try to calculate 2*2, you don't expect infinitely many answers, do you? If a product needs a parameter, it's not a product of two shapes, it's a function of two shapes and a parameter.
These are not even cartesian products! In the Euclidean space, they overlap with the cartesian product, but the current symbols for these products are ## and #* (for prism and comb products). One notes that the cartesian product does not encompass all products, because ** pyramid products and *# tegum product are not cartesian under any stretch of the imagination. Nor is the general () spheration.
Current symbols? You made up those products yourself. Not that there's anything wrong with making up products, but yours have nothing to do with this forum, at least not until you explain them in a way we can understand. Maybe cartesian product was the wrong term to use, I'm not sure what the product is I'm thinking of.
It seems like we're not talking about the same torus product, so this argument is kind of redundant. I don't understand any of your products, and you refuse to define any of them, so I don't think I'm doing anything wrong by keeping our old definitions.
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
oh pw. sorry to interrupt your heroic defense.
but. on one hand you got full pocket of 'right, wrong, must and cannot' types of judgements of operations you don't understand, which you admit several times, lastly:
that's two hands full of uncertainty.
which makes it hard to back up all the certainty that you manifest in defending 'the right' type of product.
also,
you say
arent you ? who do you mean by we when you use 'our' ? can you name those guys ? or who do you identify with in this case ?
oh. sorry to interrupt this discussion riping discussion. go on. but please pay attention to what others write when they do. perceive more than conceive. at least until those 2 functions get into balance.
but. on one hand you got full pocket of 'right, wrong, must and cannot' types of judgements of operations you don't understand, which you admit several times, lastly:
. on the other hand, you write of your own understanding:I don't understand any of your products
I'm not sure what the product is I'm thinking of.
that's two hands full of uncertainty.
which makes it hard to back up all the certainty that you manifest in defending 'the right' type of product.
also,
is a precise point.'It seems like we're not talking about the same torus product...'
you say
? are you serious ? this thread is over 40 posts long, many of it dealing with that. also, there is POLYGLOSS, which also gives relevant information on this issue. did you look up the products there as well? do you try to understand or to defend old forms of knowledge ? if the latter is true, change it. you write:you refuse to define any of them,...
I don't think I'm doing anything wrong by keeping our old definitions.
arent you ? who do you mean by we when you use 'our' ? can you name those guys ? or who do you identify with in this case ?
oh. sorry to interrupt this discussion riping discussion. go on. but please pay attention to what others write when they do. perceive more than conceive. at least until those 2 functions get into balance.
- thigle
- Tetronian
- Posts: 390
- Joined: Fri Jul 29, 2005 5:00 pm
- Location: Usa
The products are defined in terms of radiant functions, and in terms of the surtope consist.
That is, regardless of what shape the sqaure pyramid is, it is still a square pyramid. One can, for a one-inch square, place the vertex _anywhere_ above the plane, and it is _still_ a square pyramid.
The pyramid product has an altitude: that is, the product sign has dimension as well. There is nothing unusual about this.
The products never were allocated symbols. The thing was always described in text. In practice, the symbol ought be a list operator, eg rss(a,b), rather than a×b.
One notes that a product gives f(AB) = f(A)f(B). The surtope products (pyramid, tegum, prism, comb) do exactly this for the surtope algebra. The coherent products (tegum, prism, sphere) do this for the content.
We note, that when i multiply, under a coherent product, a volume X and a volume Y, i get a volume XY. In products that have a centre (eg tegum, sphere), this is independent of the position of the centre.
One notes that to spherate a figure is not a product, since you are not actually multiplying anything! It's a function, as s(A). It does not create holes. What it does do is to give substance to thin things: a perfectly flat circle becomes a solid disk that you can fumble with.
The torus product as I defined it does create holes. Specifically, it creates an internal hole, and an external hole, the nature of these have the same dimensionality as the two bases of the product.
That is, regardless of what shape the sqaure pyramid is, it is still a square pyramid. One can, for a one-inch square, place the vertex _anywhere_ above the plane, and it is _still_ a square pyramid.
The pyramid product has an altitude: that is, the product sign has dimension as well. There is nothing unusual about this.
When you try to calculate 2*2, you don't expect infinitely many answers, do you? If a product needs a parameter, it's not a product of two shapes, it's a function of two shapes and a parameter.
The products never were allocated symbols. The thing was always described in text. In practice, the symbol ought be a list operator, eg rss(a,b), rather than a×b.
One notes that a product gives f(AB) = f(A)f(B). The surtope products (pyramid, tegum, prism, comb) do exactly this for the surtope algebra. The coherent products (tegum, prism, sphere) do this for the content.
We note, that when i multiply, under a coherent product, a volume X and a volume Y, i get a volume XY. In products that have a centre (eg tegum, sphere), this is independent of the position of the centre.
One notes that to spherate a figure is not a product, since you are not actually multiplying anything! It's a function, as s(A). It does not create holes. What it does do is to give substance to thin things: a perfectly flat circle becomes a solid disk that you can fumble with.
The torus product as I defined it does create holes. Specifically, it creates an internal hole, and an external hole, the nature of these have the same dimensionality as the two bases of the product.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
I don't understand any of your products
. on the other hand, you write of your own understanding:I'm not sure what the product is I'm thinking of.
that's two hands full of uncertainty.
The product I was thinking of is a very general product defined in terms of tensors somehow. I can't remember the name, but it takes two objects and gives a third, like our products. The difference is that this product depends on where the objects are. For instance, circle*circle can be a sphere, a torus or a duocylinder, depending on what plane the circles are in. I thought it was called the cartesian product, but the cartesian product is a product of sets. Maybe the term has two meanings.
The torus product is different, because it's shift-independent. Circle#circle will always be a torus. The x product that we often use is also different, because it always puts the two objects in entirely different dimensions e.g. one circle in the xy plane, the other circle in the zw plane.
Quote:
you refuse to define any of them,...
? are you serious ? this thread is over 40 posts long, many of it dealing with that. also, there is POLYGLOSS, which also gives relevant information on this issue. did you look up the products there as well? do you try to understand or to defend old forms of knowledge ? if the latter is true, change it. you write:
I'm talking about a precise mathematical definition, like my torus product which is defined with vectors. I can't find anything like that in the polygloss. I don't even know if Wendy ever uses vectors.
The products are defined in terms of radiant functions, and in terms of the surtope consist.
Radiant functions aren't in google or in the polygloss. Is it just a function of the radius?
The products never were allocated symbols. The thing was always described in text. In practice, the symbol ought be a list operator, eg rss(a,b), rather than a×b.
Your products were only defined in text. My torus product has a vector definition, and a process for calculating parametric and cartesian equations. It's only defined for objects that it can handle without blowing up and having infinitely many solutions. It also has a purpose, namely to define the rotopes.
One notes that a product gives f(AB) = f(A)f(B).
You've got two products and a function there.
One notes that to spherate a figure is not a product, since you are not actually multiplying anything! It's a function, as s(A). It does not create holes. What it does do is to give substance to thin things: a perfectly flat circle becomes a solid disk that you can fumble with.
It's not a product in the sense of being a binary operation. It's more of a special case of a product, with the condition that the second object has to be a sphere that exists in the normal space of the first. You could also write it as a function that of an object and an integer, but it's more intuitive to see it as a product. The more general product is useless for classifying shapes, which is what we're doing.
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
The torus product is different, because it's shift-independent. Circle#circle will always be a torus. The x product that we often use is also different, because it always puts the two objects in entirely different dimensions e.g. one circle in the xy plane, the other circle in the zw plane.
This is more a fait of the circle's symmetry than the torus product. The torus product does shift, but the circle makes it less noticable.
I'm talking about a precise mathematical definition, like my torus product which is defined with vectors. I can't find anything like that in the polygloss. I don't even know if Wendy ever uses vectors.
I use vectors (eg stott-vectors in PG). But the PG does not cover the products, less so the radiant function, for various reasons. Most of the products are not exactly easy to define in a text like the PG. But i think there are entries like surtope-product, coherent-product etc in the PG.
On f(AB) = f(A)f(B): You've got two products and a function there.
Actually, it's a property of a figure is the product of the properties of the factors.
It's not a product in the sense of being a binary operation.
Then don't call it a product. If it's not freely open, then it is not a product, really, is it?
The more general product is useless for classifying shapes, which is what we're doing.
First you tell me it does not exist, and then you are kind of splitting hairs as to whether a square/circle torus has this feature or that, based on whether it has flat faces or not.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
This is more a fait of the circle's symmetry than the torus product. The torus product does shift, but the circle makes it less noticable.
What do you mean it does shift? I said it's shift independent. That is, if you shift A or B around or rotate them, it has no effect on A#B.
Then don't call it a product. If it's not freely open, then it is not a product, really, is it?
It's a restricted product. It's a special case of a more general product, with the property that for any rotopes A and B, A#B will also be a rotope. It has other nice properties as well. I don't know the definition for the more general product, because I think it uses tensors.
First you tell me it does not exist, and then you are kind of splitting hairs as to whether a square/circle torus has this feature or that, based on whether it has flat faces or not
Flat faces have nothing to do with it. There is only one circular torus. There are infinitely many square torii. The general product will take a particular circle and a particular square, and gives you one of these square torii. The same product could give you a crind, or any number of hideous shapes noone asked for. But there is no product that takes "circle" and multiplies it by "square".
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
It's a restricted product. It's a special case of a more general product, with the property that for any rotopes A and B, A#B will also be a rotope. It has other nice properties as well. I don't know the definition for the more general product, because I think it uses tensors.
The torus-product has nothing at all to do with Marek's rototopes. Many of these are spherous (topological spheres), while no torus is spherous. There may be an intersection though, but don't assume that the rototope algebra is the same as the torus product.
Flat faces have nothing to do with it. There is only one circular torus. There are infinitely many square torii.
There are infinitely many tri-circular torus. The tetratorus and the tiger are examples. The flat-face argument is no different to the preserving of the topological torus of the bi-circular prism in the tiger. Ok?
But there is no product that takes "circle" and multiplies it by "square".
Suppose you have shape A. This has a surface, and some notional centre. Take shape B, and place it so that exactly one point of the surface of B intersects with the surface of A, and the intersection of the spaces holding A and B is a line passing through the centre of A.
One then substitutes for the centre of A, an orthogonal through A that spans AB (that is, one can from the set of vectors in A, and a set of vectors in the orthogonal, create by sum, any vector that can be created by A and B together).
One then passes a ray from the orthogonal, to the surface of B, a copy of the surface of A, scaled relative to the lengths of this vector and the original vector of intersection.
The resulting surface, then is a closed product of the surfaces of A and B, such that for every point a in A, and b in B, there exists a point ab, on the surface of AB, and that for every point ab, there is a unique pairing a, b in AB. That is, the torus is a product of surfaces.
One further notes, that there is a hole (ie non-vanishing sphere), formed by the interior of B, that lies wholy inside AB, and that there is a hole (non-vanishing sphere), that lies completely outside AB, caused by the interior of A.
For example, if one supposes a {12}{5} torus, one starts with a dodecagon. At a corner, one places a pentagon. Through every point of this pentagon, there is a scaled copy of the dodecagon, parallel to the plane of the dodecagon, and having a centre common to the perpendicular of the dodecagon. The figure is bounded by 60 squares.
One notes that there is an interior hole, that creates circles parallel to the tread of the tyre, that can not expand or contract to disappear without crossing the surface. Such a circle can be prevented by inserting a pentagonal internal wall.
There is an exterior hole. This is created by the interior of the dodecahedron, and runs where the axle would run. The circle ties through the axle-hole, and around the wall of the tyre. One can prevent such a circle from forming by adding a hedrid (dodecagon) to stop these circles from forming.
The topological surface of this is then 1hh, the two h's represent the two holes, and also that the genus of a surface is twice the number of holes.
W
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
For example, if one supposes a {12}{5} torus, one starts with a dodecagon. At a corner, one places a pentagon. Through every point of this pentagon, there is a scaled copy of the dodecagon, parallel to the plane of the dodecagon, and having a centre common to the perpendicular of the dodecagon. The figure is bounded by 60 squares.
Ok, what if you take all 12 pentagons, and rotate them around their axis by one degree? You get a different shape that could still be described as a {12}{5} torus, and has exactly the same construction.
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
There are infinitely many tri-circular torus. The tetratorus and the tiger are examples. The flat-face argument is no different to the preserving of the topological torus of the bi-circular prism in the tiger. Ok?
Does this mean you admit the tetratorus and tiger are different objects?
I've had another look at your construction, but I think you'll have to be more precise.
Suppose you have shape A. This has a surface, and some notional centre. Take shape B, and place it so that exactly one point of the surface of B intersects with the surface of A
the intersection of the spaces holding A and B is a line passing through the centre of A.
I think I see what you're doing here. You're trying to position B without using the normal space of A. This isn't a good idea, because it makes your product shift-dependent. That is, if you change your origin, you get ugly non-circular shapes.
One then substitutes for the centre of A, an orthogonal through A that spans AB (that is, one can from the set of vectors in A, and a set of vectors in the orthogonal, create by sum, any vector that can be created by A and B together).
Ok, do you mean an orthogonal as in, a line perpendicular to something? If so, perpendicular to what? How can a single line span a manifold? Spanning is what a set of vectors does to a vector space. Is AB the product of A and B, A#B?
One then passes a ray from the orthogonal, to the surface of B, a copy of the surface of A, scaled relative to the lengths of this vector and the original vector of intersection.
This isn't the kind of process you can explain in one sentence.
One further notes, that there is a hole (ie non-vanishing sphere), formed by the interior of B, that lies wholy inside AB, and that there is a hole (non-vanishing sphere), that lies completely outside AB, caused by the interior of A.
All I can say is, good luck proving that without algebra or calculus.
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
Does this mean you admit the tetratorus and tiger are different objects?
No, they're the same object with different params.
I think I see what you're doing here. You're trying to position B without using the normal space of A. This isn't a good idea, because it makes your product shift-dependent. That is, if you change your origin, you get ugly non-circular shapes.
So? After all, you can construct parallelopieds from the prism product.
Ok, do you mean an orthogonal as in, a line perpendicular to something? If so, perpendicular to what? How can a single line span a manifold? Spanning is what a set of vectors does to a vector space. Is AB the product of A and B, A#B?
Orthogonal and perpendicular are set to different meanings. In orthogonal, every line of space A, is perpendicular to every line of B. For perpendicular, only some lines need be right-angled. Walls are perpendicular to the floor, but not orthogonal to it. In 3d, only a line can be orthogonal to a plane.
This isn't the kind of process you can explain in one sentence.
So? We don't have the necessary words to. A torus product is the extended product of surfaces. Each point in the surface of A, and each point in the surface of B, is paired with a point in the surface of AB. It's a bidirectional relation: A, B <--> AB. That's the essence of a product.
All I can say is, good luck proving that without algebra or calculus.
There's enough bi-pass in mathematics to avoid both of algebra and calculus. For example, the intersection of circles suffices to do all of the heavy stuff in spheric and hyperbolic geometry.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
No, they're the same object with different params.
So these two equations are equivalent, for some values of a, b, R, p, q, S?
Tiger: (sqrt(x^2 + y^2) - a)^2 + (sqrt(z^2 + w^2) - b)^2 = R^2
3-torus: (sqrt( (sqrt(x^2 + y^2) - p)^2 + z^2) - q)^2 + w^2 = S^2
There's enough bi-pass in mathematics to avoid both of algebra and calculus.
No there isn't. You can imagine these shapes, and make claims about their structure, but you can't prove or define anything without using real maths.
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
Let's see here: rss = root-sum-square = square root of the sum of squares.
You can build a torus from a previous prism, by supposing that an axis becomes a circle, ie z -> rss(y,z)-A
A circle is 1 = rss(x,y). We add a new dimension z, to get a torus.
torus: 1 = rss(rss(x,y)-K, z)
In four dimensions, we suppose that we replace an other axis in like manner: thus,
x: 1 = rss(rss(rss*x,y)-K, w-L), z)
If you replace z with a torusing axis, you get
1 = rss(rss(x,y)-K, rss(w,z)-L))
Which is pretty much the same equation, because both describe a circle-circle torus, bent into the shape of the torus. In the first instance, the axis of bend is in the xy plane, and the thing looses its circular symmetry, in the second case, the bend produces a thing with a bi-circular symmetry, because there is no loss of symmetry in the bend.
W
You can build a torus from a previous prism, by supposing that an axis becomes a circle, ie z -> rss(y,z)-A
A circle is 1 = rss(x,y). We add a new dimension z, to get a torus.
torus: 1 = rss(rss(x,y)-K, z)
In four dimensions, we suppose that we replace an other axis in like manner: thus,
x: 1 = rss(rss(rss*x,y)-K, w-L), z)
If you replace z with a torusing axis, you get
1 = rss(rss(x,y)-K, rss(w,z)-L))
Which is pretty much the same equation, because both describe a circle-circle torus, bent into the shape of the torus. In the first instance, the axis of bend is in the xy plane, and the thing looses its circular symmetry, in the second case, the bend produces a thing with a bi-circular symmetry, because there is no loss of symmetry in the bend.
W
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
You've got a random * in your equations, and an L in the wrong place. Here's the correct equations using rss:
3-torus: 1 = rss(rss(rss(x,y)-K, w) - L, z)
tiger: 1 = rss(rss(x,y)-K, rss(w,z)-L))
Pretty much the same? They're completely different equations, with a few irrelevent similarities. There's no reason to call them the same object here.
"circle-circle torus" is a description of the equation (and a bad one), not the other way around.
3-torus: 1 = rss(rss(rss(x,y)-K, w) - L, z)
tiger: 1 = rss(rss(x,y)-K, rss(w,z)-L))
Which is pretty much the same equation
Pretty much the same? They're completely different equations, with a few irrelevent similarities. There's no reason to call them the same object here.
both describe a circle-circle torus, bent into the shape of the torus.
"circle-circle torus" is a description of the equation (and a bad one), not the other way around.
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
can someone put both of those equations in regulare form? preferably with <sup>1/2</sup> for square roots, and <sup>2</sup> for squares. instead of sqt and ^2 respectively. i understand it perfectly... its just that the argument that they are similare is more easily understood with the proper formulas. (i'd do it myself but im uber buisy)
too many people have self replicating sigs. Don't copy this.
- batmanmg
- Trionian
- Posts: 201
- Joined: Sun Aug 20, 2006 10:21 pm
Tiger: ((x<sup>2</sup> + y<sup>2</sup>)<sup>1/2</sup> - a)<sup>2</sup> + ((z<sup>2</sup> + w<sup>2</sup>)<sup>1/2</sup> - b)<sup>2</sup> = R<sup>2</sup>
3-torus: ( ( ( (x<sup>2</sup>+ y<sup>2</sup>)<sup>1/2</sup> - p)<sup>2</sup> + z<sup>2</sup>)<sup>1/2</sup> - q)<sup>2</sup> + w<sup>2</sup> = S<sup>2</sup>
3-torus: ( ( ( (x<sup>2</sup>+ y<sup>2</sup>)<sup>1/2</sup> - p)<sup>2</sup> + z<sup>2</sup>)<sup>1/2</sup> - q)<sup>2</sup> + w<sup>2</sup> = S<sup>2</sup>
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
Maybe they could be similar in this way:
Tetratorus is generated by rotating a torus around a non-intersecting vertical plane (perpendicular to its main circle).
Tiger is generated by rotating a torus around a non-intersecting horizontal plane (parallel to its main circle).
So, if we take the vertical plane and move it to horizontal position, taking a snapshot of the resulting shape at each instant, we have a continuous transformation of tetratorus into tiger, right?
Tetratorus is generated by rotating a torus around a non-intersecting vertical plane (perpendicular to its main circle).
Tiger is generated by rotating a torus around a non-intersecting horizontal plane (parallel to its main circle).
So, if we take the vertical plane and move it to horizontal position, taking a snapshot of the resulting shape at each instant, we have a continuous transformation of tetratorus into tiger, right?
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Who is online
Users browsing this forum: No registered users and 45 guests
