Building a Toratope by Rotations from a Circle
52 posts
• Page 2 of 2 • 1, 2
Re: Building a Toratope by Rotations from a Circle
So if you want to do it that way, we would have
S1#(S2xS3) = (S1#S2)xS3 = ((III)I)(III)
S1#(S3xS2) = (S1#S3)xS2 = ((IIII)I)(II)
I'm still opposed to trying to extend the definition in this way. It doesn't bring us any new shapes, it's not clear exactly how the vector algebra definition should be extended, and it requires arbitrary symmetry breaking. The original definition of spheration is like a geometric interpretation of the unit cotangent bundle. It's not clear what the new definition is doing, if anything. We're just kind of assuming rules for it.
Besides, there's another restriction on the spheration operator. If there are too many dimensions in the normal space, then spheration is undefined. For example,
(S1xS1xS1) # S1 doesn't exist. You're starting with (II)(II)(II), and you want to put brackets around it in such a way that there are only two things in the brackets. You can have (S1xS1xS1) # S2 or (S1xS1xS1) # S3 or more, but not (S1xS1xS1) # S1.
S1#(S2xS3) = (S1#S2)xS3 = ((III)I)(III)
S1#(S3xS2) = (S1#S3)xS2 = ((IIII)I)(II)
I'm still opposed to trying to extend the definition in this way. It doesn't bring us any new shapes, it's not clear exactly how the vector algebra definition should be extended, and it requires arbitrary symmetry breaking. The original definition of spheration is like a geometric interpretation of the unit cotangent bundle. It's not clear what the new definition is doing, if anything. We're just kind of assuming rules for it.
Besides, there's another restriction on the spheration operator. If there are too many dimensions in the normal space, then spheration is undefined. For example,
(S1xS1xS1) # S1 doesn't exist. You're starting with (II)(II)(II), and you want to put brackets around it in such a way that there are only two things in the brackets. You can have (S1xS1xS1) # S2 or (S1xS1xS1) # S3 or more, but not (S1xS1xS1) # S1.
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
Re: Building a Toratope by Rotations from a Circle
So if you want to do it that way, we would have
S1#(S2xS3) = (S1#S2)xS3 = ((III)I)(III)
S1#(S3xS2) = (S1#S3)xS2 = ((IIII)I)(II)
Wouldn't it be
S2#(S1xS2) = (S2#S1)xS2 = ((III)I)(III)
S3#(S1xS1) = (S3#S1)xS1 = ((IIII)I)(II) ?
And, yeah, the dual definitions probably aren't necessary. If the notation can currently define them with one sequence, then there is no need for two. Just a thought on the commutative relationship. But if you mean both of the definitions for min-frames, then how else would you describe min-frames, such as the 3-frame ((II)I)(II) embedded in 5D? It is a valid surface, which can be defined algebraically, apart from open and closed toratopes.
Besides, there's another restriction on the spheration operator. If there are too many dimensions in the normal space, then spheration is undefined. For example,
(S1xS1xS1) # S1 doesn't exist. You're starting with (II)(II)(II), and you want to put brackets around it in such a way that there are only two things in the brackets. You can have (S1xS1xS1) # S2 or (S1xS1xS1) # S3 or more, but not (S1xS1xS1) # S1.
Yes, this is true.
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: Building a Toratope by Rotations from a Circle
Wouldn't it be
S2#(S1xS2) = (S2#S1)xS2 = ((III)I)(III)
S3#(S1xS1) = (S3#S1)xS1 = ((IIII)I)(II) ?
No, I'm looking at two different combination of the same three different spheres: S1, S2, S3. I might have made a mistake in the notation on the RHS but not on the left.
EDIT: I did make a mistake. I should have said
S1#(S2xS3) = (S1#S2)xS3 = ((II)II)(IIII)
S1#(S3xS2) = (S1#S3)xS2 = ((II)III)(III)
These are topologically equivalent, but geometrically very different. You can't convert one to another by a rotation.
But if you mean both of the definitions for min-frames, then how else would you describe min-frames, such as the 3-frame ((II)I)(II) embedded in 5D? It is a valid surface, which can be defined algebraically, apart from open and closed toratopes.
Usually when I think of any toratope I'm thinking of the min-frame. If you want to be specific about the frame, you use the frame notation. In general, if I talk about a cube, that could mean anything from a solid physical block of matter to 8 points. It's only when I say an "F_1 cube" that you know I'm actually talking about 12 lines arranged in the edges of a cube. When we talk about duocylinder it's the same issue, it can mean three different things. But it's easy to specify which one we mean if we want to. So it's not a problem. It's certainly not a reason to redefine # to make things more specific but also more confusing.
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
Re: Building a Toratope by Rotations from a Circle
Okay, that works. So, taking (S1#S3)xS2 = ((II)III)(III) , for example, to spherate with a circle, would you enclose the min-frame with an additional pair of brackets, and add #S1 to the end, as in ((S1#S3)xS2)#S1 ?
Since I have an algorithm to derive the frames of non-toratopes, I'll adopt the frame notation when describing them. So, take the cone IO>, for example:
F_3 cone : IO>
F_2 cone : IO , (O)>
F_1 cone : (O)
F_0 cone : *
which goes together in the frame polynome IO> • {IO + (O)>} • (O) • * • n
where IO is the circle base, (O)> is the curved 2-surface of the cone (the disk-edge pyramid) , (O) is the 1D disk edge , and * is the 0D point.
Since I have an algorithm to derive the frames of non-toratopes, I'll adopt the frame notation when describing them. So, take the cone IO>, for example:
F_3 cone : IO>
F_2 cone : IO , (O)>
F_1 cone : (O)
F_0 cone : *
which goes together in the frame polynome IO> • {IO + (O)>} • (O) • * • n
where IO is the circle base, (O)> is the curved 2-surface of the cone (the disk-edge pyramid) , (O) is the 1D disk edge , and * is the 0D point.
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: Building a Toratope by Rotations from a Circle
Defining "frames" rigorously isn't trivial. It has something to do with the set of points in the higher frame that aren't smooth. I remember I came close to defining it once.
-

PWrong - Pentonian
- Posts: 1599
- Joined: Fri Jan 30, 2004 8:21 am
- Location: Perth, Australia
Re: Building a Toratope by Rotations from a Circle
I’d like to introduce another systematic mathematical notation for toratopes in any number of dimensions and a systematic nomenclature based on it that I've developed. It's short and by standards of high dimensional geometry it's easy to understand. A drawback is that it is not ambiguous, i.e. there are different ways to write down the object of one the same topology, but one can choose a convention.
But first the important question that bothers me: Are the ditorus and the tiger topolocically one and the same object, i.e. can one be deformed into another without breaking it or turning it inside out? I’m tending to the answer yes, but I don’t have a way to proof or disproof it. Their surface just seems to be the same in every aspect I can think of. It would be cool to find a criterium to tell if two arbitrary toratopes are topolocially the same, i.e. if there are really 33 different toratopes in 6D or less.
But first the important question that bothers me: Are the ditorus and the tiger topolocically one and the same object, i.e. can one be deformed into another without breaking it or turning it inside out? I’m tending to the answer yes, but I don’t have a way to proof or disproof it. Their surface just seems to be the same in every aspect I can think of. It would be cool to find a criterium to tell if two arbitrary toratopes are topolocially the same, i.e. if there are really 33 different toratopes in 6D or less.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Building a Toratope by Rotations from a Circle
Teragon wrote:I’d like to introduce another systematic mathematical notation for toratopes in any number of dimensions and a systematic nomenclature based on it that I've developed. It's short and by standards of high dimensional geometry it's easy to understand.
All right! Let's see it. I also made my own a while back, independently of toratope notation, which I learned afterwards. It was using my older, linear way of constructing shapes, that resembles more of a fiber bundle sequence. It was also somewhat ambiguous, though I added some new notations that could define some apart, but not all of them. It broke down in 6D with some shapes, like the 6D torus of a 5D cylspherintigroid, (((II)II)(II)) or ((III)((II)I)) .
Teragon wrote:Are the ditorus and the tiger topolocically one and the same object, i.e. can one be deformed into another without breaking it or turning it inside out?
Yes, they're the same, topologically. But, different geometrically (non-isometric). Not sure how you can prove it, either. Maybe show how they're both a surface of revolution of a torus? Perhaps borrow some insight on their formulas for surface volume and bulk? Marek14 computed these already , using Pappus' Centroid Theorem. The formulas are the same for both, only their radius parameters have different values.
Teragon wrote:It would be cool to find a criterium to tell if two arbitrary toratopes are topolocially the same
Actually, Keiji was using a method involving graphs that defined topo equivalents. Each graph of yellow nodes and edges represent two or more toratopes that can be transformed into each other, by turning inside out some way. This property can also be seen clearly enough, in toratope notation.
Topological Duals:
((III)I) and ((II)II)
((II)(II)) and (((II)I)I)
Topo Trios:
(((III)I)I) and (((II)II)I) and (((II)I)II)
(((III)II)I) and (((III)I)II) and (((II)II)II)
(((II)I)(II)) and (((II)(II))I) and ((((II)I)I)I)
I think ((III)(II)) and ((II)(II)I) are duals, but I'm not 100% sure.
Teragon wrote:... i.e. if there are really 33 different toratopes in 6D or less
Oh, there definitely are 33 unique types in 6D, but only 6D, and only according to a specific way to construct shapes from a 2D circle (different combos of bisecting and non-bisecting rotation into n+1D, around coordinate planes only). More important, these are all possible geometric varieties, ignoring all things topologically.
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: Building a Toratope by Rotations from a Circle
ICN5D, thanks for the fast reply.
Let's talk only about toratopes constructed using those two operations. It's nice to see that Keiji came to the same number of topologically different objects in 6D as I did with my approach (13). This suggests that from my notation you can immediately tell if two toratopes are topological duals and you should be able to find a formula calculating the total number of different topologies in any number of dimensions. It seems that there are objects that are topologically different in d dimensions, but the the same in d+1 dimensions.
It's been a while since I've learned your notation. I don't get the difference between ((II)(II)I) and (((II)(II))I) right now, but as ((III)(II)) contains a 3-loop and ((II)(II)I) doesn't, they can't be duals. (or does it?).
I disagree that the torisphere and the spheritorus are topological equivalents. How would you deform a spherical cavity into a circular one?
Edit: Changed part of my post after Marek posted his answer.
Let's talk only about toratopes constructed using those two operations. It's nice to see that Keiji came to the same number of topologically different objects in 6D as I did with my approach (13). This suggests that from my notation you can immediately tell if two toratopes are topological duals and you should be able to find a formula calculating the total number of different topologies in any number of dimensions. It seems that there are objects that are topologically different in d dimensions, but the the same in d+1 dimensions.
ICN5D wrote:I think ((III)(II)) and ((II)(II)I) are duals, but I'm not 100% sure.
It's been a while since I've learned your notation. I don't get the difference between ((II)(II)I) and (((II)(II))I) right now, but as ((III)(II)) contains a 3-loop and ((II)(II)I) doesn't, they can't be duals. (or does it?).
ICN5D wrote:Topological Duals:
((III)I) and ((II)II)
I disagree that the torisphere and the spheritorus are topological equivalents. How would you deform a spherical cavity into a circular one?
Edit: Changed part of my post after Marek posted his answer.
Last edited by Teragon on Wed Dec 13, 2017 1:35 pm, edited 3 times in total.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Building a Toratope by Rotations from a Circle
Teragon wrote:ICN5D, thanks for the fast reply.
Let's talk only about toratopes constructed using those two operations. It's nice to see that Keiji came to the same number of topologically different objects in 6D as I did with my approach (13). This suggests that from my notation you can immediately tell if two toratopes are topological duals and you could calculate the total number of different topologies in any number of dimensions.ICN5D wrote:I think ((III)(II)) and ((II)(II)I) are duals, but I'm not 100% sure.
It's been a while since I've learned your notation. I don't get the difference between ((II)(II)I) and (((II)(II))I) right now, but as ((III)(II)) contains a 3-loop and ((II)(II)I) doesn't, they can't be duals. (or does it?)
As for the difference between ((II)(II)I) and (((II)(II))I):
The first, "221-tiger", is based on the 4D product of two circles. You take this product, and then you take a set of points that all have the same distance from that figure. If you do this in 4D, you get the standard tiger, ((II)(II)). If you do this in 5D, then 221-tiger will result. If you do this in 6D, you'll get the 222-tiger, ((II)(II)II).
221-tiger, like normal 4D tiger, has three radii: Two radii of the two circles it's based on, and a third radius that determines the distance of its points from the base figure.
The second one, "tiger torus", is more complicated. It has the full tiger, ((II)(II)), as its base figure, and it's comprised of points that have a set distance from the surface of that tiger. In 4D, this would just result in two disjoint tigers, but in 5D, this will result in a new figure. Since tiger has 3 radii and we are adding a new degree of freedom, a fourth radius appears. (As a rule of thumb, the number of radii of a toratope is the same as the number of parentheses pairs in its notation.)
I could describe the 4D mid-cuts, but for easier understanding, it will be probably better to have a look at their 3D mid-cuts which are easier to visualize.
As they are 5D objects, they each have 10 3D-midcuts.
For 221-tiger, these are:
Vertical stack of two toruses x4 (further divided in two sets with major radius of torus and separation switched, if the two relevant radii are not the same)
Empty set x2
Four spheres in rectangular formation x4
For torus tiger, these are:
Vertical stack of two minor pairs of toruses (a "minor" pair signifies that they have the same major diameter but differ in their minor diameters, so one is completely inside the other) x4 (with the same caveat that two have one combination of major radius/separation and two have the other one)
Empty set x2
Four toruses in rectangular formation x4
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Building a Toratope by Rotations from a Circle
Thank you Marek14, this was far more than I needed. It was just not clear, to which extensions of the tiger both expressions correspond.
Ok, so ((II)(II)I) does contain a spherical loop too. Still I think ((III)(II)) and ((II)(II)I) are topologically different, at least in 5D. You can't exchange the innermost loop with any of the outer loops. You can't exchange the two loops of the torus in 3D either, except if you add one more dimension, so that there is no closed cavity anymore.
Ok, so ((II)(II)I) does contain a spherical loop too. Still I think ((III)(II)) and ((II)(II)I) are topologically different, at least in 5D. You can't exchange the innermost loop with any of the outer loops. You can't exchange the two loops of the torus in 3D either, except if you add one more dimension, so that there is no closed cavity anymore.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Building a Toratope by Rotations from a Circle
Teragon wrote:I disagree that the torisphere and the spheritorus are topological equivalents. How would you deform a spherical cavity into a circular one?
Teragon wrote:You can't exchange the two loops of the torus in 3D either, except if you add one more dimension, so that there is no closed cavity anymore.
Both of these can be answered, or so I believe, by looking at this animation:

See what's going on here? Specifically with the major and minor radius? When the torus turns inside out, the major becomes the minor, while the minor becomes the major. They switch roles.
So, what if we have a torisphere : ((III)I) , with a circular minor, and a spherical major radius? What do you think will happen when we puncture and turn inside out? The sphere switches roles with the circle, and it becomes a spheritorus ((II)II) with a sphere-shaped minor and circle-shaped major radius.
Teragon wrote:Still I think ((III)(II)) and ((II)(II)I) are topologically different, at least in 5D. You can't exchange the innermost loop with any of the outer loops.
Well, according to the above points, this is what will happen, but perhaps only with certain shapes. The real question is if the role switching happens when we have +2 major radii (the entire class of 'tigroids')?
That's why I'm not sure. If the minor can become a major radius, can this happen with ((III)(II)) turned into ((II)(II)I) ? If it can't happen with tigroids, then a good question is why not?
Teragon wrote:It's been a while since I've learned your notation. I don't get the difference between ((II)(II)I) and (((II)(II))I) right now
Oh, it's not mine. I just came along one day and learned it from marek. Mine looks like IO(OO) , IOO(O) , IO(O)(O) , IO(O)[(O)] .
But in addition to what marek said, you can also imagine them apart by how to construct them. A few more things:
• ((II)(II)I) can be made by using a ((II)II) , sphere over circle, and shifting vertically along the z-axis, then revolving into 5D.
• If ((II)(II)) is circle over 'tiger frame' (tiger frame = flat torus / clifford torus), then ((II)(II)I) is 2-sphere over tiger frame. Likewise, ((II)(II)II) is 3-sphere over tiger frame, ((II)(II)III) is 4-sphere over tiger frame, etc.
• (((II)(II))I) can be made by using a (((II)I)I) , torus over circle, and shifting vert along z, then revolve into 5D.
• If ((II)(II)) is circle over 'tiger frame' , then (((II)(II))I) is torus over tiger frame (one of two ways), or also circle over a whole tiger.
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: Building a Toratope by Rotations from a Circle
ICN5D wrote:Teragon wrote:I disagree that the torisphere and the spheritorus are topological equivalents. How would you deform a spherical cavity into a circular one?Teragon wrote:You can't exchange the two loops of the torus in 3D either, except if you add one more dimension, so that there is no closed cavity anymore.
Both of these can be answered, or so I believe, by looking at this animation:
See what's going on here? Specifically with the major and minor radius? When the torus turns inside out, the major becomes the minor, while the minor becomes the major. They switch roles.
No, it's not allowed to cut a hole into the surface! As soon as you do this, you are creating an object with a different topology.
ICN5D wrote:The real question is if the role switching happens when we have +2 major radii (the entire class of 'tigroids')?
I'd say switching (without cutting a hole) is possible between all loops except for the first / smallest / innermost. When you want to exchange two loops what you have to do is bring them into a position, where they are "orthogonal" to each other (I'll explain later in detail what I mean by this). As the smallest loop contains all dimensions, this is not possible in this case, except, if the dimensionality of the hyperspace is at least two dimensions larger than the surface of the toratope is. Then we have that extra direction that is needed.
You can also understand it with the cavity, the closed hole of the toratope. If you would exchange the innermost loop with another loop of different dimensionality, the cavity would always have to change its topology. You get it by contracting the innermost loop (set r = 0). The spheritorus has a toroidal cavity, the torisphere has a spherical one. You can't deform a torus into a sphere without cutting a hole and reconnecting the ends.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Building a Toratope by Rotations from a Circle
The question is: is cutting the hole in torus absolutely necessary to invert it, or is it just a trick to make it work in 3D? In other words, if you had more dimensions available, could you turn the torus inside out without cutting it?
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Building a Toratope by Rotations from a Circle
Marek14 wrote:The question is: is cutting the hole in torus absolutely necessary to invert it, or is it just a trick to make it work in 3D? In other words, if you had more dimensions available, could you turn the torus inside out without cutting it?
It is absolutely necessary in 3D, but yes, if you had more dimensions, you could turn it inside out. The same is true for the torisphere and the spheritorus.
I actually don't know if the notion of a topology is defined relative to a given number of dimensions or if you can add a dimension in order to deform it. It would really make sense to define it independ of the number of dimensions. I mean, a spheritorus is still a spheritorus in 5D. In this case, torisphere and the spheritorus would indeed be equivalent.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Building a Toratope by Rotations from a Circle
Teragon wrote:Marek14 wrote:The question is: is cutting the hole in torus absolutely necessary to invert it, or is it just a trick to make it work in 3D? In other words, if you had more dimensions available, could you turn the torus inside out without cutting it?
It is absolutely necessary in 3D, but yes, if you had more dimensions, you could turn it inside out. The same is true for the torisphere and the spheritorus.
I actually don't know if the notion of a topology is defined relative to a given number of dimensions or if you can add a dimension in order to deform it. It would really make sense to define it independ of the number of dimensions. I mean, a spheritorus is still a spheritorus in 5D. In this case, torisphere and the spheritorus would indeed be equivalent.
Well, imagine that you are a 3D being (should be easy) living in the 3D surface of torisphere/spheritorus. Is there any way, without measuring diameters, to determine whether it's a torisphere or spheritorus?
Surface of normal 3D torus can be considered to have the same topology as Clifford torus (product of two circles in 4D) -- but 3D torus is deformed in order to fit one dimension lower. The same way, torisphere and spheritorus can be considered deformed examples of the 5D product of sphere and circle.
This, of course, depends on whether you consider toratopes as surfaces or as solid bodies.
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Building a Toratope by Rotations from a Circle
Marek14 wrote:Well, imagine that you are a 3D being (should be easy) living in the 3D surface of torisphere/spheritorus. Is there any way, without measuring diameters, to determine whether it's a torisphere or spheritorus?
Okay, well yes there is a difference. If you go around the 2-loop of a spheritorus, it has always the same circumference, no matter where you are on the 1-loop. If you go around the 2-loop of a torisphere, its size depends on the position on the 1-loop. If you go around the 1-loop of a spheritorus, its size depends on the position on the on the 2-loop. If you go around the 1-loop of a torisphere, it has always the same circumference, no matter where you are on the 2-loop. I wouldn't say that this implies they are topologically different though, as distances can be compressed and stretched.
The point is how the mathematical definition is. It would be good to have a mathematician here. I'm just recalling that a mirror image of a chiral 3D object is considered to have a different topology, but through their mutual mirror symmetry they are in some way connatural. In 4D, they would have one and the same topology. One could take on a similar view for objects like the spheritorus and the torisphere. Their topologies are different in 4D, but they are connected through an inside-out-turn that can be done in 5D without breaking the surface.
If we would consider them to be solid it would become easier. They would be different in any number of dimensions then (I think).
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Building a Toratope by Rotations from a Circle
All right, here's my thinking. If we can use 5D space to transform a tiger into a 3-torus, and vice versa:
((II)(II)) <--> (((II)I)I)
then, using a 6D space, should we be able to turn ((II)(II)I) into (((II)I)II) ?
If this is the case, would we also be allowed to turn (((II)I)II) into ((III)(II)) ?
((II)(II)) <--> (((II)I)I)
then, using a 6D space, should we be able to turn ((II)(II)I) into (((II)I)II) ?
If this is the case, would we also be allowed to turn (((II)I)II) into ((III)(II)) ?
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: Building a Toratope by Rotations from a Circle
ICN5D wrote:All right, here's my thinking. If we can use 5D space to transform a tiger into a 3-torus, and vice versa:
((II)(II)) <--> (((II)I)I)
then, using a 6D space, should we be able to turn ((II)(II)I) into (((II)I)II) ?
If this is the case, would we also be allowed to turn (((II)I)II) into ((III)(II)) ?
Logically, surface of any toratope should be topologically equivalent to some product of spheres of various dimensions. From the toratope notation, you can read the "signature", as number of terms inside the various parentheses. Both (((II)I)II) and ((III)(II)) would have the same signature, 223 (circle x circle x sphere, 2 fundamental circular loops and 1 fundamental spherical envelope), so they could be transformed.
For 5D toratopes, the signatures are:
5: (IIIII)
42: ((IIII)I), ((II)III)
33: ((III)II)
322: (((III)I)I), (((II)II)I), ((III)(II)), (((II)I)II), ((II)(II)I)
2222: ((((II)I)I)I), (((II)(II))I), (((II)I)(II))
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Building a Toratope by Rotations from a Circle
ICN5D wrote:All right, here's my thinking. If we can use 5D space to transform a tiger into a 3-torus, and vice versa:
((II)(II)) <--> (((II)I)I)
You only need 4D for that, because the loops of both are the same. Its just like deforming a duocircle into a torus in 4D.
ICN5D wrote:then, using a 6D space, should we be able to turn ((II)(II)I) into (((II)I)II) ?
Again, 5D are enough to do this. It's the same as for the 4D case, except there is another dimension in which the inner loop extends as a sphere.
ICN5D wrote:If this is the case, would we also be allowed to turn (((II)I)II) into ((III)(II)) ?
Here we really need to turn the torus inside out using 6D, because the outer loops, that define the shape of the cavity are different.
If the innermost loops are identical and the rest of the loops are the same, but have different configurations, the toratopes can be transformed into each other without an additional dimension. If the toratopes have the same loops in different configurations and the innermost loops are different, one has to be turned inside out in some way and an additional dimension is needed.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Building a Toratope by Rotations from a Circle
So here is an overview of toratopes up to 6D.
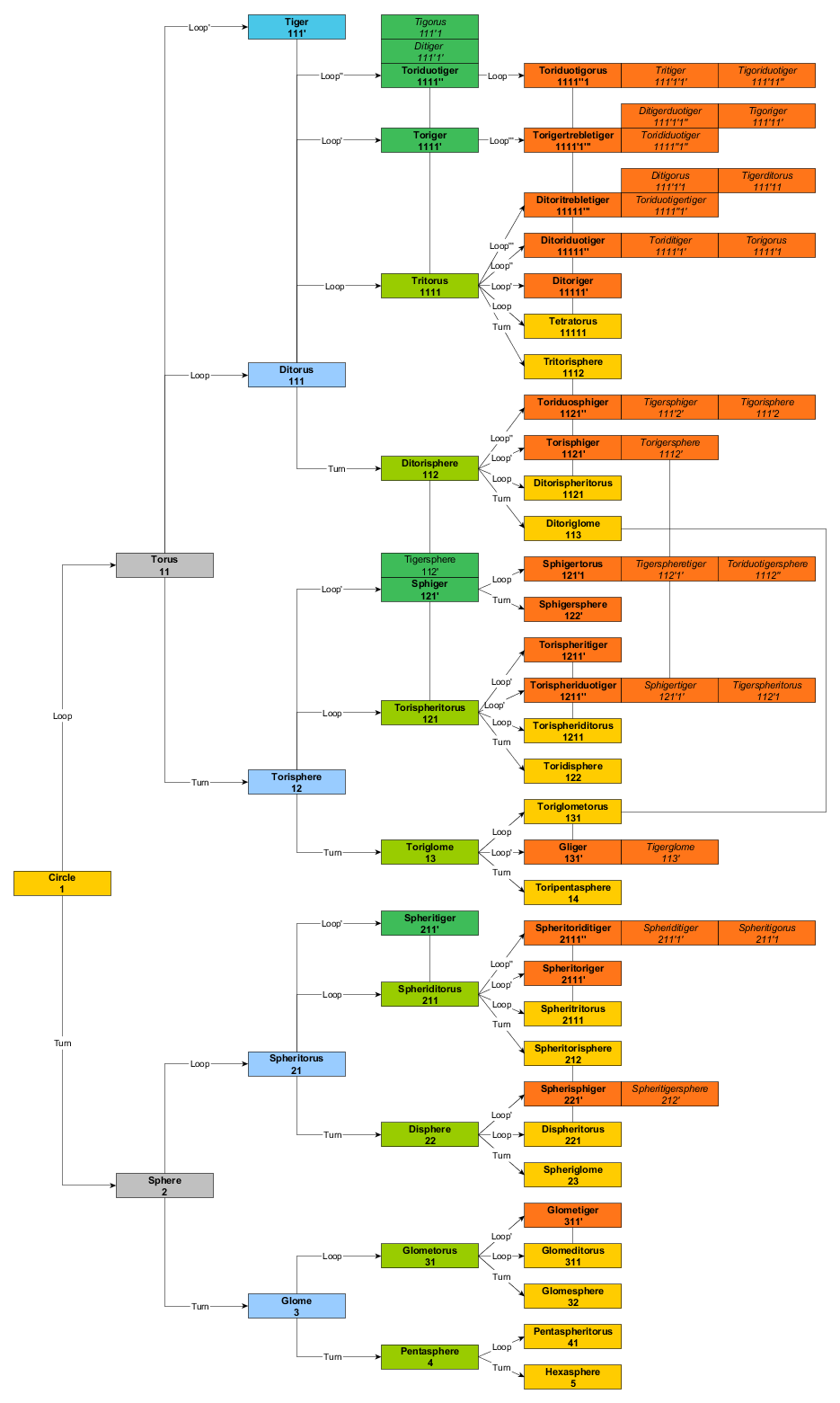
I’m differentiating between three types of toratopes: Ordered ones, orthogonal ones and flat ones. In order to keep it overseeable and because those obviously have not been accounted for in this thread, I’ve left the flat toratopes apart in the diagram. Ordered toratopes have no apostrophes (') in their names while orthogonal toratopes do.
In my notation, the digits represent the different loops from the smallest to the largest, compatible with the naming already established in 4D (spheritorus = 21), and their values represent the dimensionalities of the loops. The dimensionality of a loop is the number of directions you can go on the surface of the toratope revolving around the center of the specific loop. The dimensionality of the whole object’s hypersurface is the sum of all numbers and must be less than the dimensionality of space they live in.
In ordered toratopes, the loops have an unambiguous order defined by their radii that can’t be changed without changing the geometry of the object or leading to self-intersection. For L1L2L3: R1 < R2 < R3. Orthogonal toratopes contain two or more loops that are orthogonal to each other, which means either loop can assume the larger radius, leading to an ambiguity in the naming. L1L2' = L2L1': R1 < or = or > L2. Flat toratopes are also orthogonal and only exist in a hyperspace that has at least two dimensions more than their hypersurface. The simplest example is the duocircle (Clifford torus).
All basic toratopes may be created by doing a sequence of the following two operations starting with a circle:
1.) Bisecting rotation (called “rotation” in the diagram): By applying this operation you increase the dimensionality of the largest loop by one. A circle (1-loop) becomes a sphere (2-loop), a sphere becomes a glome (3-loop) and so on.
2.) Rotation around a point outside of the toratope (called “loop” in the diagram): By applying this operation you create a new loop, i.e. add a new number to the sequence. In many case there are several ways to do this, leading to objects with different geometries. In the diagram, only the way of construction from the next lower dimensional ordered toratope is drawn.
Lines with no label connect objects with identical topology (in the space of lowest dimensionality they can exist in), but different geometry. Fields that are touching each other correspond to different names for one and the same object, arising from the different possible pathways of constructing it due to the interchangeability of some of its loops.
Further explanations will follow.

I’m differentiating between three types of toratopes: Ordered ones, orthogonal ones and flat ones. In order to keep it overseeable and because those obviously have not been accounted for in this thread, I’ve left the flat toratopes apart in the diagram. Ordered toratopes have no apostrophes (') in their names while orthogonal toratopes do.
In my notation, the digits represent the different loops from the smallest to the largest, compatible with the naming already established in 4D (spheritorus = 21), and their values represent the dimensionalities of the loops. The dimensionality of a loop is the number of directions you can go on the surface of the toratope revolving around the center of the specific loop. The dimensionality of the whole object’s hypersurface is the sum of all numbers and must be less than the dimensionality of space they live in.
In ordered toratopes, the loops have an unambiguous order defined by their radii that can’t be changed without changing the geometry of the object or leading to self-intersection. For L1L2L3: R1 < R2 < R3. Orthogonal toratopes contain two or more loops that are orthogonal to each other, which means either loop can assume the larger radius, leading to an ambiguity in the naming. L1L2' = L2L1': R1 < or = or > L2. Flat toratopes are also orthogonal and only exist in a hyperspace that has at least two dimensions more than their hypersurface. The simplest example is the duocircle (Clifford torus).
All basic toratopes may be created by doing a sequence of the following two operations starting with a circle:
1.) Bisecting rotation (called “rotation” in the diagram): By applying this operation you increase the dimensionality of the largest loop by one. A circle (1-loop) becomes a sphere (2-loop), a sphere becomes a glome (3-loop) and so on.
2.) Rotation around a point outside of the toratope (called “loop” in the diagram): By applying this operation you create a new loop, i.e. add a new number to the sequence. In many case there are several ways to do this, leading to objects with different geometries. In the diagram, only the way of construction from the next lower dimensional ordered toratope is drawn.
Lines with no label connect objects with identical topology (in the space of lowest dimensionality they can exist in), but different geometry. Fields that are touching each other correspond to different names for one and the same object, arising from the different possible pathways of constructing it due to the interchangeability of some of its loops.
Further explanations will follow.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Building a Toratope by Rotations from a Circle
Interesting, I see what you're doing. The table represents different ways of constructing one shape to another, while being organized into topological equals. In this case, a bisecting rotation is called your 'turn' , and non-bisecting is your 'loop' , of which you've assigned many varieties of a loop. And the sequences are similar to a fiber bundle notation.
An idea I had a while ago was an add-on to S^1 x S^1 x S^1 to differentiate between a tiger, 3-torus, torus of a flat 2-torus, or a flat 3-torus. All 4 of these surfaces fit the bill. It looks like your notation is including something similar (loop' , loop'', etc), that tells things apart in a somewhat geometric way.
And so they can! Thanks. I guess the same thing can be reasoned from the homology holes method you and Pwrong were doing. It was the 'pulling out the diameters' method, or expanding them or something to that effect. It went like :
(((III)I)(II)) -> (((III)I)I)(II) -> (((III)I)(II)(II) -> (III)(II)(II)(II)
And I suppose the various combinations in between would be topological equals.
An idea I had a while ago was an add-on to S^1 x S^1 x S^1 to differentiate between a tiger, 3-torus, torus of a flat 2-torus, or a flat 3-torus. All 4 of these surfaces fit the bill. It looks like your notation is including something similar (loop' , loop'', etc), that tells things apart in a somewhat geometric way.
Marek14 wrote:Logically, surface of any toratope should be topologically equivalent to some product of spheres of various dimensions. From the toratope notation, you can read the "signature", as number of terms inside the various parentheses. Both (((II)I)II) and ((III)(II)) would have the same signature, 223 (circle x circle x sphere, 2 fundamental circular loops and 1 fundamental spherical envelope), so they could be transformed.
For 5D toratopes, the signatures are:
5: (IIIII)
42: ((IIII)I), ((II)III)
33: ((III)II)
322: (((III)I)I), (((II)II)I), ((III)(II)), (((II)I)II), ((II)(II)I)
2222: ((((II)I)I)I), (((II)(II))I), (((II)I)(II))
And so they can! Thanks. I guess the same thing can be reasoned from the homology holes method you and Pwrong were doing. It was the 'pulling out the diameters' method, or expanding them or something to that effect. It went like :
(((III)I)(II)) -> (((III)I)I)(II) -> (((III)I)(II)(II) -> (III)(II)(II)(II)
And I suppose the various combinations in between would be topological equals.
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: Building a Toratope by Rotations from a Circle
ICN5D, exactly. I just thought, writing “non-bisecting rotation” is too long for the diagram.
When we do a non-bisecting rotation (add a loop), there are in general different ways to do that. My approach is based on the concept of orthogonality. By making use of it, we obviate the need for brackets (at least for non-flat toratopes) and gain insights about the structure of different toratopes. For those who have not yet thought about it in a similar way, it's a rather lengthy way through careful deliberations, but it pays off. I’m not sure how detailed it should be, as different readers have very different geometry and math backgrounds.
So what do I mean, when I say, two loops are orthogonal to each other? Each loop is associated with a certain dimensionality. It corresponds to the number of linearly independent vectors at any point of the toratope leading around that specific loop (tangent vectors). As any linear combination of those independent tangent vectors gives a new tangent vector and as a toratope consists of an infinite number of points, each of its loop has also an infinite number of tangent vectors.
For example, the sphere (2) is a 2-loop, i.e. it has two linearly independent tangent vectors at any point on the surface. Depending on the position on the sphere, the vectors can point anywhere in space. The torus (11) is composed of two loops, each with one tangent vector. While the vector associated with the small loop can point anywhere in space, the vector of the loop with the large radius can only assume directions in the xy-plane.
We can understand the relationships between the different loops of a toratope by considering what happens when we build it dimension by dimension. If we do a (bisecting or non-bisecting) rotation, we are just adding a new tangent vector to the toratope, tracing out the plane of our rotation. This means we are creating a continuous rotational symmetry between one direction the toratope is already extended in and a new direction. As a consequence, any tangent vector of any loop pointing along the direction lying in the plane of rotation, will give rise to a set of tangent vectors pointing anywhere in the rotational plane. Depending on the direction we choose to rotate into the new coordinate, the resulting toratope may look different.
Definition: Two loops are orthogonal to each other, if all the tangent vectors of one are orthogonal to all the tangent vectors of another, i.e. if their scalar product is zero.
We can write down toratopes in terms of the rotational (hyper-)planes of every loop (unfortunately I'm not able to produce clear spaces in order to align identical coordinates vertically):
XYZ
ZW
This is a spheritorus (21). We start with a 1-loop (tangent vectors in XY) and do a bisecting rotation in the XZ or YZ plane (both are equivalent because of the spherical symmetry of the loop) to create a 2-loop (tangent vectors in XYZ). Then we do a non-bisecting rotation to create a new loop (every paragraph corresponds to one loop). It doesn’t matter if we do it in XW, YW or ZW, the resulting object is always a spheritorus because of the spherical symmetry of the first loop. As the first loop contains one coordinate of the second loop (Z), it also contains the second coordinate of the new loop (W). Its tangent vectors now encompass XYZW.
If we continue and add another loop, there are two possibilities:
XYZ
ZW
WU
(Spheriditorus - 211)
or
XYZ
ZW
X U
(Spheritiger - 211’)
Either we do a non-intersecting rotation in the ZU- or WU-plane. The first and the second loop then share a coordinate with the third loop. Their (hyper-)planes intersect the plane of the new rotation and so they rotate with the new loop around a new center point that lies inside their hyperplane.
Or we do a non-intersecting rotation in the XU- or YU-plane. In this case the plane of rotation intersects the first loop, but not the second. The second and the third loop are thus orthogonal to each other. This means the second loop rotates around a point in a direction that lies outside of its hyperplane.
If two loops are orthogonal to each other, none of the tangent vectors of one point towards the center of another. If two loops are orthogonal, the sizes of their radii are only confined by the sizes of the next non-orthogonal loops. They are interchangeable in the sense that no matter which one is created first, the resulting object is geometrically the same. The mathematical term “commutable” describes it nicely. Two loops commute with each other, if changing their order does not change the geometry of the toratope. We can use the terms orthogonal and commutable interchangeably to describe the structure of a toratope.
While the topology of a toratope can be characterized by the number and dimensionality of its loops, its geometry can be characterized by orthogonality relations between the individual loops, i.e. which ones are orthogonal to which. Enough for today, I’ll explain how the structure of a toratope is reflected in the naming another time.
When we do a non-bisecting rotation (add a loop), there are in general different ways to do that. My approach is based on the concept of orthogonality. By making use of it, we obviate the need for brackets (at least for non-flat toratopes) and gain insights about the structure of different toratopes. For those who have not yet thought about it in a similar way, it's a rather lengthy way through careful deliberations, but it pays off. I’m not sure how detailed it should be, as different readers have very different geometry and math backgrounds.
So what do I mean, when I say, two loops are orthogonal to each other? Each loop is associated with a certain dimensionality. It corresponds to the number of linearly independent vectors at any point of the toratope leading around that specific loop (tangent vectors). As any linear combination of those independent tangent vectors gives a new tangent vector and as a toratope consists of an infinite number of points, each of its loop has also an infinite number of tangent vectors.
For example, the sphere (2) is a 2-loop, i.e. it has two linearly independent tangent vectors at any point on the surface. Depending on the position on the sphere, the vectors can point anywhere in space. The torus (11) is composed of two loops, each with one tangent vector. While the vector associated with the small loop can point anywhere in space, the vector of the loop with the large radius can only assume directions in the xy-plane.
We can understand the relationships between the different loops of a toratope by considering what happens when we build it dimension by dimension. If we do a (bisecting or non-bisecting) rotation, we are just adding a new tangent vector to the toratope, tracing out the plane of our rotation. This means we are creating a continuous rotational symmetry between one direction the toratope is already extended in and a new direction. As a consequence, any tangent vector of any loop pointing along the direction lying in the plane of rotation, will give rise to a set of tangent vectors pointing anywhere in the rotational plane. Depending on the direction we choose to rotate into the new coordinate, the resulting toratope may look different.
Definition: Two loops are orthogonal to each other, if all the tangent vectors of one are orthogonal to all the tangent vectors of another, i.e. if their scalar product is zero.
We can write down toratopes in terms of the rotational (hyper-)planes of every loop (unfortunately I'm not able to produce clear spaces in order to align identical coordinates vertically):
XYZ
ZW
This is a spheritorus (21). We start with a 1-loop (tangent vectors in XY) and do a bisecting rotation in the XZ or YZ plane (both are equivalent because of the spherical symmetry of the loop) to create a 2-loop (tangent vectors in XYZ). Then we do a non-bisecting rotation to create a new loop (every paragraph corresponds to one loop). It doesn’t matter if we do it in XW, YW or ZW, the resulting object is always a spheritorus because of the spherical symmetry of the first loop. As the first loop contains one coordinate of the second loop (Z), it also contains the second coordinate of the new loop (W). Its tangent vectors now encompass XYZW.
If we continue and add another loop, there are two possibilities:
XYZ
ZW
WU
(Spheriditorus - 211)
or
XYZ
ZW
X U
(Spheritiger - 211’)
Either we do a non-intersecting rotation in the ZU- or WU-plane. The first and the second loop then share a coordinate with the third loop. Their (hyper-)planes intersect the plane of the new rotation and so they rotate with the new loop around a new center point that lies inside their hyperplane.
Or we do a non-intersecting rotation in the XU- or YU-plane. In this case the plane of rotation intersects the first loop, but not the second. The second and the third loop are thus orthogonal to each other. This means the second loop rotates around a point in a direction that lies outside of its hyperplane.
If two loops are orthogonal to each other, none of the tangent vectors of one point towards the center of another. If two loops are orthogonal, the sizes of their radii are only confined by the sizes of the next non-orthogonal loops. They are interchangeable in the sense that no matter which one is created first, the resulting object is geometrically the same. The mathematical term “commutable” describes it nicely. Two loops commute with each other, if changing their order does not change the geometry of the toratope. We can use the terms orthogonal and commutable interchangeably to describe the structure of a toratope.
While the topology of a toratope can be characterized by the number and dimensionality of its loops, its geometry can be characterized by orthogonality relations between the individual loops, i.e. which ones are orthogonal to which. Enough for today, I’ll explain how the structure of a toratope is reflected in the naming another time.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
52 posts
• Page 2 of 2 • 1, 2
Who is online
Users browsing this forum: No registered users and 47 guests
