What is the difference between a torisphere and a spheritorus?
I don't understand the explanation in wiki
Torisphere and spheritorus
14 posts
• Page 1 of 1
Torisphere and spheritorus
People may consider as God the beings of finite higher dimensions,
though in truth, God has infinite dimensions
though in truth, God has infinite dimensions
-

Prashantkrishnan - Trionian
- Posts: 114
- Joined: Mon Jan 13, 2014 5:37 pm
- Location: Kochi, Kerala, India
Re: Torisphere and spheritorus
By reading the wiki, I infer that spheration of a cubinder gives a spheritorus, which I am unable to believe (not that I understand what spheration is  ).
).
I don't get the connection between a cubinder and a spheritorus, as we obtain a spheritorus from the spherinder.
 ).
).I don't get the connection between a cubinder and a spheritorus, as we obtain a spheritorus from the spherinder.
People may consider as God the beings of finite higher dimensions,
though in truth, God has infinite dimensions
though in truth, God has infinite dimensions
-

Prashantkrishnan - Trionian
- Posts: 114
- Joined: Mon Jan 13, 2014 5:37 pm
- Location: Kochi, Kerala, India
Re: Torisphere and spheritorus
I'm not exactly sure if the "spheration" there means a specific operation. Simply said:
Mathematically, a normal 3D torus is set of points in 3D with a given distance from a circle. Torisphere and spheritorus are directly derived from that: torisphere is set of points in 4D with given distance from a sphere, while spheritorus is a set of points with given distance from a circle, like torus (but in 4D).
If you take a loop of string in 4D, it would be the spheritorus. If you'd make a hollow sphere out of something in 4D, it would approximate the torisphere.
You can find some cuts and videos in the toratope subforum. One interesting thing is that torisphere and spheritorus can be joined together like links in chain, which is not possible with two torispheres or two spheritoruses.
You can also make both spheritorus and torisphere by rotating a torus along a bisecting plane.
Mathematically, a normal 3D torus is set of points in 3D with a given distance from a circle. Torisphere and spheritorus are directly derived from that: torisphere is set of points in 4D with given distance from a sphere, while spheritorus is a set of points with given distance from a circle, like torus (but in 4D).
If you take a loop of string in 4D, it would be the spheritorus. If you'd make a hollow sphere out of something in 4D, it would approximate the torisphere.
You can find some cuts and videos in the toratope subforum. One interesting thing is that torisphere and spheritorus can be joined together like links in chain, which is not possible with two torispheres or two spheritoruses.
You can also make both spheritorus and torisphere by rotating a torus along a bisecting plane.
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Torisphere and spheritorus
Marek14 wrote:Mathematically, a normal 3D torus is set of points in 3D with a given distance from a circle.
This is slightly troublesome to understand.
If we consider a torus whose equatorial plane is the XY plane, where would this circle be, for which all points in the torus are at a given distance? How would it be oriented? And how can you measure the distance of points from a circle in 3D, if the points lie all around the circle? (Some of the points would have to lie on the same plane as the circle)
I observe that if you replace points in a circle by circles (in realmspace) we get a torus. Do you mean that we replace the centre also with a circle? If so, how?
Marek14 wrote:You can also make both spheritorus and torisphere by rotating a torus along a bisecting plane.
From this explanation, I infer that if we rotate the torus (which I mentioned above) around the XY plane, we get a torisphere and if we rotate it around the YZ or ZX plane we get a spheritorus.
Also, does any part of the spheritorus look like a duocylinder?

Considering the plane along which a torus is cut to give this shape, observing how any other cross section of the torus, which is a circle not on the plane of rotation, reminds me of some curved version of the duocylinder.
The explanation of the torisphere in the wiki is as follows
The torisphere, previously known as the toraspherinder, is a four-dimensional torus formed by taking an uncapped spherinder and connecting its ends through its inside.
Why would we need to use the inside of the spherinder?
Your explanation of the torisphere reminds me of the explanation of spheritorus in the wiki. My confusion here is mainly because I am not understanding how there can be a locus of points at a given distance from a circle or a sphere in 3D and in 4D respectively.
People may consider as God the beings of finite higher dimensions,
though in truth, God has infinite dimensions
though in truth, God has infinite dimensions
-

Prashantkrishnan - Trionian
- Posts: 114
- Joined: Mon Jan 13, 2014 5:37 pm
- Location: Kochi, Kerala, India
Re: Torisphere and spheritorus
Distance from a circle is pretty simple -- you must take the circle as only the edge, not the full disc. If you take a circle in 2D and take points that have a certain small distance from this circle, you'll get two more circles; one outside, one inside. The original circle of radius R will give you two additional circles of radii R+r and R-r.
This is a cut of torus. If you look at the parallel slices of torus in this direction, they are all pairs of concentric circles. The further you are from the mid-cut plane, the closer the circles will be, until, at the distance of r, they merge into a single circle and vanish.
Both torisphere and spheritorus have analogical sets of 3D slices. The torisphere slices all look like pairs of concentric spheric shells, which come closer together as you move from the mid-cut hyperplane, merge into a single sphere and vanish. The spheritorus slices look like normal 3D torus whose major radius stays the same, but the minor radius shrinks as you move from the mid-cut hyperplane, until it's reduced to zero, making the torus into a circle, and vanish.
A torus can be imagined as an "inflated circle", with every point of a circle replaced with another circle perpendicular to the original circle. In this analogy, spheritorus would replace each point of a circle with spherical shell and torisphere would replace each point of sphere with a circle.
Your rotation ideas for torus are correct.
I don't think spheritorus looks like a duocylinder, but there is a toratope (the tiger) that is derived from it.
There are multiple ways of deriving the toratopes; one of them is that each toratope is a particular rotation of a lower-dimensional one. The rotations are very easy to see in the toratopic notation, as they can be mechanically derived by character manipulation.
In 3D, you can only rotate a circle, written as (II) in the toratopic notation.
You can either make a bisecting rotation, which takes a I and replaces it with II, and you'll get (III), which is a sphere.
Or you can make a nonbisecting rotation, around a line that doesn't intersect the circle, and that replaces I with (II), getting ((II)I), the torus. This is why a torus has a mid-cut that looks like two separated circles.
In 4D, you can rotate two 3D things: a sphere (III) or a torus ((II)I).
Bisecting rotation of sphere is (IIII), a glome.
Nonbisecting rotation of sphere is ((II)II), a spheritorus. That's where the spheritorus mid-cut of two separated spheres comes from.
Rotation of torus is more complicated because torus has two non-equivalent positions of I symbols, which is another way to say that it has two distinct types of coordinate planes.
Bisecting rotation of torus can be ((III)I), a torisphere, or ((II)II), a spheritorus. Both of these have a mid-cut that is a single torus.
Nonbisecting rotation of torus adds additional complexity to the shape. It results in (((II)I)I), a ditorus, or ((II)(II)), a tiger.
This is a cut of torus. If you look at the parallel slices of torus in this direction, they are all pairs of concentric circles. The further you are from the mid-cut plane, the closer the circles will be, until, at the distance of r, they merge into a single circle and vanish.
Both torisphere and spheritorus have analogical sets of 3D slices. The torisphere slices all look like pairs of concentric spheric shells, which come closer together as you move from the mid-cut hyperplane, merge into a single sphere and vanish. The spheritorus slices look like normal 3D torus whose major radius stays the same, but the minor radius shrinks as you move from the mid-cut hyperplane, until it's reduced to zero, making the torus into a circle, and vanish.
A torus can be imagined as an "inflated circle", with every point of a circle replaced with another circle perpendicular to the original circle. In this analogy, spheritorus would replace each point of a circle with spherical shell and torisphere would replace each point of sphere with a circle.
Your rotation ideas for torus are correct.
I don't think spheritorus looks like a duocylinder, but there is a toratope (the tiger) that is derived from it.
There are multiple ways of deriving the toratopes; one of them is that each toratope is a particular rotation of a lower-dimensional one. The rotations are very easy to see in the toratopic notation, as they can be mechanically derived by character manipulation.
In 3D, you can only rotate a circle, written as (II) in the toratopic notation.
You can either make a bisecting rotation, which takes a I and replaces it with II, and you'll get (III), which is a sphere.
Or you can make a nonbisecting rotation, around a line that doesn't intersect the circle, and that replaces I with (II), getting ((II)I), the torus. This is why a torus has a mid-cut that looks like two separated circles.
In 4D, you can rotate two 3D things: a sphere (III) or a torus ((II)I).
Bisecting rotation of sphere is (IIII), a glome.
Nonbisecting rotation of sphere is ((II)II), a spheritorus. That's where the spheritorus mid-cut of two separated spheres comes from.
Rotation of torus is more complicated because torus has two non-equivalent positions of I symbols, which is another way to say that it has two distinct types of coordinate planes.
Bisecting rotation of torus can be ((III)I), a torisphere, or ((II)II), a spheritorus. Both of these have a mid-cut that is a single torus.
Nonbisecting rotation of torus adds additional complexity to the shape. It results in (((II)I)I), a ditorus, or ((II)(II)), a tiger.
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Torisphere and spheritorus
"Spheration" is a surface-finish. It converts thin lines into tubes, points into spheres, etc. Have a look at http://www.atomium.be/ , which is a spherated cube and centre.
In 3d, a torus is a spherated circle. This means you take a circle, and turn it into a snake-like thing.
In 4d, a torisphere, is a 'spherated sphere' . This means you take a hollow sphere in the XYZ space, where R is a radius, and replace the points on the R surface by a circle in the WR plane. In other words, you replace the thin edge of the sphere with a much thicker boundary, such as formed by a clay model.
A spheritorus is made by 'spherating a circle'. This means that you take a circle in the WX plane, and fatten it up to make a solid thing. This makes a point into a sphere in the RYZ space, so you get a lot of sphere disks, rather like disks in a juke box. The way you form it from the sperinder is to imagine a spheric prism, (in the XYZ plane, a sphere, in the W space, a line), and then convert the thing into a loop, by bending the spherinder into a circle in the XW space.
In 3d, a torus is a spherated circle. This means you take a circle, and turn it into a snake-like thing.
In 4d, a torisphere, is a 'spherated sphere' . This means you take a hollow sphere in the XYZ space, where R is a radius, and replace the points on the R surface by a circle in the WR plane. In other words, you replace the thin edge of the sphere with a much thicker boundary, such as formed by a clay model.
A spheritorus is made by 'spherating a circle'. This means that you take a circle in the WX plane, and fatten it up to make a solid thing. This makes a point into a sphere in the RYZ space, so you get a lot of sphere disks, rather like disks in a juke box. The way you form it from the sperinder is to imagine a spheric prism, (in the XYZ plane, a sphere, in the W space, a line), and then convert the thing into a loop, by bending the spherinder into a circle in the XW space.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Torisphere and spheritorus
wendy wrote:"Spheration" is a surface-finish. It converts thin lines into tubes, points into spheres, etc.
In tetraspace, does this mean converting thin lines into spherinders, points into glomes and planes into cubinders?
This is how I would have to take it to interpret spheration of circle in 3D and in 4D differently.
People may consider as God the beings of finite higher dimensions,
though in truth, God has infinite dimensions
though in truth, God has infinite dimensions
-

Prashantkrishnan - Trionian
- Posts: 114
- Joined: Mon Jan 13, 2014 5:37 pm
- Location: Kochi, Kerala, India
Re: Torisphere and spheritorus
Prashantkrishnan wrote:wendy wrote:"Spheration" is a surface-finish. It converts thin lines into tubes, points into spheres, etc.
In tetraspace, does this mean converting thin lines into spherinders, points into glomes and planes into cubinders?
This is how I would have to take it to interpret spheration of circle in 3D and in 4D differently.
Yes, basically. You can imagine it as adding missing dimensions to the lower-dimensional entities.
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Torisphere and spheritorus
Marek14 wrote:Prashantkrishnan wrote:wendy wrote:"Spheration" is a surface-finish. It converts thin lines into tubes, points into spheres, etc.
In tetraspace, does this mean converting thin lines into spherinders, points into glomes and planes into cubinders?
This is how I would have to take it to interpret spheration of circle in 3D and in 4D differently.
Yes, basically. You can imagine it as adding missing dimensions to the lower-dimensional entities.
This also fills in the gap and explains the sudden mention of the cubinder!

wendy wrote:In 4d, a torisphere, is a 'spherated sphere' . This means you take a hollow sphere in the XYZ space, where R is a radius, and replace the points on the R surface by a circle in the WR plane. In other words, you replace the thin edge of the sphere with a much thicker boundary, such as formed by a clay model.
Now that seems to clarify some of the cross-sectional diagrams drawn by Polyhedron Dude
 ! At first I was confused since I thought that the sphere, being a hedrix, would produce something like a cubinder on spheration in tetraspace. Though after that as I looked at the diagrams, it seemed to be to be more similar to the curved surcell of a spherinder (analogous to the relation between the surface of the torus and the curved surface of the cylinder).
! At first I was confused since I thought that the sphere, being a hedrix, would produce something like a cubinder on spheration in tetraspace. Though after that as I looked at the diagrams, it seemed to be to be more similar to the curved surcell of a spherinder (analogous to the relation between the surface of the torus and the curved surface of the cylinder).A spheritorus is made by 'spherating a circle'. This means that you take a circle in the WX plane, and fatten it up to make a solid thing. This makes a point into a sphere in the RYZ space, so you get a lot of sphere disks, rather like disks in a juke box. The way you form it from the sperinder is to imagine a spheric prism, (in the XYZ plane, a sphere, in the W space, a line), and then convert the thing into a loop, by bending the spherinder into a circle in the XW space.
I can get the connection between the spheration of a circle and the formation of the spheritorus from the spherinder. But still, why should this be the closed toratope corresponding to the cubinder?
Marek14 wrote:Distance from a circle is pretty simple -- you must take the circle as only the edge, not the full disc. If you take a circle in 2D and take points that have a certain small distance from this circle, you'll get two more circles; one outside, one inside. The original circle of radius R will give you two additional circles of radii R+r and R-r.
This is a cut of torus. If you look at the parallel slices of torus in this direction, they are all pairs of concentric circles. The further you are from the mid-cut plane, the closer the circles will be, until, at the distance of r, they merge into a single circle and vanish.
Both torisphere and spheritorus have analogical sets of 3D slices. The torisphere slices all look like pairs of concentric spheric shells, which come closer together as you move from the mid-cut hyperplane, merge into a single sphere and vanish. The spheritorus slices look like normal 3D torus whose major radius stays the same, but the minor radius shrinks as you move from the mid-cut hyperplane, until it's reduced to zero, making the torus into a circle, and vanish.
A torus can be imagined as an "inflated circle", with every point of a circle replaced with another circle perpendicular to the original circle. In this analogy, spheritorus would replace each point of a circle with spherical shell and torisphere would replace each point of sphere with a circle.
Your rotation ideas for torus are correct.
I don't think spheritorus looks like a duocylinder, but there is a toratope (the tiger) that is derived from it.
That makes much of it clear.

There are multiple ways of deriving the toratopes; one of them is that each toratope is a particular rotation of a lower-dimensional one. The rotations are very easy to see in the toratopic notation, as they can be mechanically derived by character manipulation.
In 3D, you can only rotate a circle, written as (II) in the toratopic notation.
You can either make a bisecting rotation, which takes a I and replaces it with II, and you'll get (III), which is a sphere.
Or you can make a nonbisecting rotation, around a line that doesn't intersect the circle, and that replaces I with (II), getting ((II)I), the torus. This is why a torus has a mid-cut that looks like two separated circles.
In 4D, you can rotate two 3D things: a sphere (III) or a torus ((II)I).
Bisecting rotation of sphere is (IIII), a glome.
Nonbisecting rotation of sphere is ((II)II), a spheritorus. That's where the spheritorus mid-cut of two separated spheres comes from.
Rotation of torus is more complicated because torus has two non-equivalent positions of I symbols, which is another way to say that it has two distinct types of coordinate planes.
Bisecting rotation of torus can be ((III)I), a torisphere, or ((II)II), a spheritorus. Both of these have a mid-cut that is a single torus.
Nonbisecting rotation of torus adds additional complexity to the shape. It results in (((II)I)I), a ditorus, or ((II)(II)), a tiger.
This toratopic notation is one of the most confusing things here for me

Does this indirectly mean that getting a cylinder by rotating a square is nonbisecting rotation of II to (II)I or does the question of bisecting or nonbisecting rotation arise only for closed polytopes? And what is nonbisecting rotation? Is it the same as taking a prism of a toratope of n dimensions and making its ends meet in n + 1 dimensions?
I would be grateful to have clarifications of these.
People may consider as God the beings of finite higher dimensions,
though in truth, God has infinite dimensions
though in truth, God has infinite dimensions
-

Prashantkrishnan - Trionian
- Posts: 114
- Joined: Mon Jan 13, 2014 5:37 pm
- Location: Kochi, Kerala, India
Re: Torisphere and spheritorus
Prashantkrishnan wrote:This toratopic notation is one of the most confusing things here for me
Does this indirectly mean that getting a cylinder by rotating a square is nonbisecting rotation of II to (II)I or does the question of bisecting or nonbisecting rotation arise only for closed polytopes? And what is nonbisecting rotation? Is it the same as taking a prism of a toratope of n dimensions and making its ends meet in n + 1 dimensions?
I would be grateful to have clarifications of these.
Getting a cylinder by rotating a square is a bisecting rotation. The whole thing works perfectly only for closed toratopes.
Nonbisecting rotation simply means that you rotate a shape around a line/plane/hyperplane/whatever that doesn't pass through it. When you make a bisecting rotation of shape T, the resulting shape will have a mid-cut that is just T. When you make a nonbisecting rotation, the resulting shape will have a mid-cut that is two separated copies of T.
There are topics here about the toratopic notation. It's really a nice way to describe these shapes because it can show how to build them and how their cuts look, and I spent lots of time explaining it, so you might want to check those
 viewtopic.php?f=24&t=801 is the main one.
viewtopic.php?f=24&t=801 is the main one.- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Torisphere and spheritorus
It all seems to fit now...
But I still have one doubt.
Is there a relation between the open toratopes and the corresponding closed toratopes? (Like between the cube and the sphere or between the cylinder and the torus)
Only thing I understand about open and closed toratopes is that open toratopes of n dimensions have n-2 dimensional structures on their surface which lead to a sharp discontinuity in their n-1 dimensional surface while closed toratopes have smooth n-1 dimensional surfaces.
And I infer that the non bisecting rotations of open toratopes give rise to shapes which are not included among toratopes. Eg:-
Nonbisecting rotation of a square gives the double of what is shown in this figure:
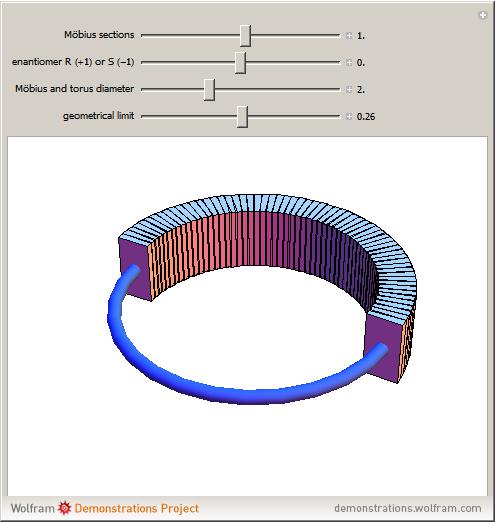
Such a figure would not be considered a toratope
But I still have one doubt.
Is there a relation between the open toratopes and the corresponding closed toratopes? (Like between the cube and the sphere or between the cylinder and the torus)
Only thing I understand about open and closed toratopes is that open toratopes of n dimensions have n-2 dimensional structures on their surface which lead to a sharp discontinuity in their n-1 dimensional surface while closed toratopes have smooth n-1 dimensional surfaces.
And I infer that the non bisecting rotations of open toratopes give rise to shapes which are not included among toratopes. Eg:-
Nonbisecting rotation of a square gives the double of what is shown in this figure:

Such a figure would not be considered a toratope
People may consider as God the beings of finite higher dimensions,
though in truth, God has infinite dimensions
though in truth, God has infinite dimensions
-

Prashantkrishnan - Trionian
- Posts: 114
- Joined: Mon Jan 13, 2014 5:37 pm
- Location: Kochi, Kerala, India
Re: Torisphere and spheritorus
The relationship between open and closed toratopes with similar notation is, I think, not really a relationship...
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Torisphere and spheritorus
Prashantkrishnan wrote:Is there a relation between the open toratopes and the corresponding closed toratopes?
Well, I think the only real relation is that a closed toratope is a spherated open toratope. In this sense, spheration is the process of adding extra parentheses around all terms of an open toratope. This will change the shape by removing certain cells, and bending/folding/smoothing the remaining cells into a toroidal ring or n-sphere.
Open
(II)I
(III)I
(III)(II)
((II)I)(III)
Closed
((II)I)
((III)I)
((III)(II))
(((II)I)(III))
Enclosing with parentheses is easy to do, but figuring out the physical transformation is a bit more abstract, and really depends on the shape. There are five different ways an open spherates into the proper closed.
• First is the hose-linking, where we join the ends of a prism into a loop.
• Second is the Sock-Roll, and just like it sounds, we bend the shape back, and roll it back onto itself. Just about all single extrusion spherations are a sock rolling.
• Third is the rounding or polishing of sharp edges and corners into a sphere. Only applies to n-cube spheration, which directly becomes an n-ball : III -> (III) , cube -> sphere
• Fourth is emptying out all n-1 flat sides, and folding a part of the rolling side. This is a special case of multiple extruded n-sphere prisms, with a square or cube product, i.e: (II)II , (III)III , (IIIIII)IIIIII . The toroidal rolling side of these shapes takes the form of an n-cube over an n-sphere. The n-cube part gets folded into an n+1 sphere, while stretched over the hollow frame. It's a difficult process to visualize, but it works with any shape that applies.
• Fifth is emptying out all n-1 surfaces, and expanding only the n-(n/2) edge. This is a special case of +4D duoprisms, like the duocylinder (II)(II) . Open toratopes that are a multiple n-sphere product, i.e. : (II)(II) , (III)(II) , (III)(II)(II) , (III)(III)(II)(IIII)(IIIIII) , etc , will all have this fifth type of spheration. For 4D duocylinder, the n-2 surface is a smoothly curving single structure. For a 6D triocylinder (II)(II)(II) , the n-3 surface (edge) is also a single smooth structure. Spherating these will impregnate the surface with an infinite amount of circles, spheres, glomes, etc.
Spherating some shapes:
Cylinder : (II)I , infinite circles along line
Spherating will make ((II)I) , a torus. We could hose link the cylinder, or sock roll into a torus. A torus is infinite circles over a circle.
Spherinder : (III)I , infinite spheres along line
Spherating will make ((III)I) , a torisphere. Only sock rolling a sphere prism will make a torisphere. This is folding the extruded 2-surface of a sphere back onto itself, and joining the "flat" spherical ends. We end up with infinite circles over a big hollow sphere. If we hose-linked a sphere prism, we'd get a spheritorus ((II)II), infinite spheres over circle.
Cubinder : (II)II , infinite circles within square, or cylinders along line
Spherating will make ((II)II) , a spheritorus. This is the weird fourth type, that bends cubes into spheres. The curved rolling side of a cubinder is square torus. By spherating, we empty out the 4 flat cylinder sides, and fold the 2D square part of the square torus, into the 2-surface of a 3d sphere. Starting with infinite squares over circle, we end up with infinite spheres over circle: the spheritorus.
Torinder : ((II)I)I , infinite torus along line, or infinite cylinders over circle
Spherating will make (((II)I)I) , a ditorus. One extrusion means hose-link and sock-rolling will turn torus prism into ditorus, infinite torus over circle.
Duocylinder : (II)(II) , infinite circles within circle
Spherating will make ((II)(II)) , a tiger. A product of two circles means we empty out the n-1 surfaces, and expand the n-2 edge. This is the single structure that two 3D tori are bound to, as the edge. And using this as a frame, we impregnate with infinite circles in every point, and make the tiger, a 4D donut ring.
Duocylinder torus / cyltorinder : ((II)I)(II) , infinite torus within circle / infinite duocylinders over circle
This is a torus of an open toratope, which combines both attributes in one. Can be built two different ways, actually. One could extrude 3D torus into 4D torus prism, then bisecting rotate into 5D cyltorinder. Or, bisecting rotate 3D cylinder into 4D duocylinder, then non-bisecting rotate into 5D duocylindric torus. Both are equal. And since this is an open toratope, we can spherate the n-2 surface. Spherating will make (((II)I)(II)) , a tiger torus, a.k.a cyltorintigroid. The 3D single structure becomes expanded with infinite circles in every point, making a 5D donut ring.
Tiger Prism : ((II)(II))I , infinite tigers along line
This is a 5D prism, made by extending a 4D tiger into 5D. It has two flat tiger endcaps, joined by a linear extension of the surface of a tiger. By spherating, we get (((II)(II))I) , a toritiger, infinite circles over tiger. The two tiger endcaps were emptied out, leaving behind a hollow tube-like linear extension of a tiger surface. Then we bent the tube back, and rolled it down to join the open ends. This process turns the linear surface extension into a small circular one. In the end we get an infinite number of circles within the surface of a single tiger, and creates another 5D donut ring.
So as you can see, spheration can mean many different things. Depending on the open toratope prism, you could get a closed toratope donut ring, or a sphere. And as for the square torus in your picture, it can be a cross section of open toratopes, and can be defined by adapting the notation.
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: Torisphere and spheritorus
If you look at the picture in Prashantkrishnan's post, you would see a type of spheration under way. The thin blue line represents the circle being spherated, and the rectangular sections represent the thing being 'fleshed out' for real-world mangling. Spheration uses a circular section here, but it should give you a pretty good idea of what's going on.
It is in effect, a surface finish to the blue line to make the line stand up to the rigors of the the real world.
It is in effect, a surface finish to the blue line to make the line stand up to the rigors of the the real world.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
14 posts
• Page 1 of 1
Who is online
Users browsing this forum: No registered users and 22 guests
