mr_e_man wrote:(Notice, we couldn't have done this symmetrization so easily before I had expanded it. Or could we?)
Yes, we could!

No need to take a month to expand and simplify the 4-fold product for a spider; just leave the product as is. I'll explain.
ICN5D wrote:This plots a triangular array of 3 toruses standing on their rim. My next, more recent idea (experiment) was to define a mirror-image (upside-down) triangle array and call the 3rd variable "w" (when it's really z for the plotter) , and then compare it to this one above. Then, try to take all the terms containing w and insert them in to the equation above. It will produce a 4-variable equation that should morph between the triangular arrays by rotation on plane zw. Or, so it seems. It's an experiment I've never tried before, and it's a total shot in the dark, but could totally work, too.
You have the right idea here. It's basically what I did with the symmetry that swaps a and b (the two major radii), and swaps z and w, and rotates in the x,y-plane by 360°/(2n) (in this case 60°, thus replacing the triangle by its mirror image). But I didn't know how to enforce this symmetry and add the appropriate w terms without expanding the product.
My new approach doesn't rely on symmetry; it can take any two 3D objects as cross-sections, defined by polynomial equations F(x,y,z,0)=0 and F(x,y,0,w)=0, provided that they have the same 2D cross-section F(x,y,0,0)=0, and construct a 4D object F(x,y,z,w)=0. Of course it's not unique; any terms can be added with zw as a factor, to get a different shape.
Clearly, from the properties of polynomials, F(x,y,z,0) is exactly all of those monomials in F(x,y,z,w) that don't have w as a factor. So F(x,y,z,w) - F(x,y,z,0) is exactly all of the terms that do have w as a factor. Similarly, F(x,y,0,0) is all of the terms that have neither z nor w as a factor, and F(x,y,z,0) - F(x,y,0,0) is all of the terms that have z but not w as a factor. So we can decompose F into four components as follows:
F(x,y,z,w) = [F(x,y,0,0)] + [F(x,y,z,0) - F(x,y,0,0)] + [F(x,y,0,w) - F(x,y,0,0)] + [zw P(x,y,z,w)],
where the first component has neither z nor w, the second component has z but not w, the third component has w but not z, and the fourth component has both z and w. This can be rearranged to
F(x,y,z,w) = F(x,y,z,0) + F(x,y,0,w) - F(x,y,0,0) + zw P(x,y,z,w).
For our 2n-legged tiger, we have an array of n tori in the x,y,z-space, a different array of n tori in the x,y,w-space, and a common array of 2n circles in the x,y-plane:
F(x,y,z,0) = prod
k=0n-1( (x²+y²+z²+d²-c² - 2
A2k•
r)² - 4b²z² - 4(
b2k•
r)² )
= prod
k=0n-1( (x²+y²+z²+d²-c² - 2A(x cos(2πk/n) + y sin(2πk/n)))² - 4b²z² - 4b²(y cos(2πk/n) - x sin(2πk/n))² ),
F(x,y,0,w) = prod
k=0n-1( (x²+y²+w²+d²-c² - 2
B2k•
r)² - 4a²w² - 4(
a2k•
r)² )
= prod
k=0n-1( (x²+y²+w²+d²-c² - 2B(x cos(π(2k+1)/n) + y sin(π(2k+1)/n)))² - 4a²w² - 4a²(x sin(π(2k+1)/n) - y cos(π(2k+1)/n))² ),
F(x,y,0,0) = prod
k=02n-1( x²+y²+d²-c² - 2
dk•
r )
= prod
k=0n-1 (x²+y²+d²-c² - 2
d2k•
r) (x²+y²+d²-c² - 2
d2k-1•
r).
(Now how can I rewrite that dot product...
d2k•
r =
A2k•
r +
b2k•
r= (a + b cos(π/n))/sin(π/n) (x cos(2πk/n) + y sin(2πk/n)) + b (y cos(2πk/n) - x sin(2πk/n))
= (ax cos(2πk/n) + bx cos(2πk/n + π/n) + ay sin(2πk/n) + by sin(2πk/n + π/n)) / sin(π/n)
= (a (x cos(2kπ/n) + y sin(2kπ/n)) + b (x cos((2k+1)π/n) + y sin((2k+1)π/n))) / sin(π/n),
d2k-1•
r =
A2k•
r -
b2k•
r= (a + b cos(π/n))/sin(π/n) (x cos(2πk/n) + y sin(2πk/n)) - b (y cos(2πk/n) - x sin(2πk/n))
= (ax cos(2πk/n) + bx cos(2πk/n - π/n) + ay sin(2πk/n) + by sin(2πk/n - π/n)) / sin(π/n)
= (a (x cos(2kπ/n) + y sin(2kπ/n)) + b (x cos((2k-1)π/n) + y sin((2k-1)π/n))) / sin(π/n). )
So we add the two n-fold products, and subtract the 2n-fold product, and finally add (or subtract) some z²w² terms, to get an equation for a 2n-legged tiger. But this doesn't work well for the ordinary 4-legged tiger; the "remainder" is fully 8th degree, with lots of terms that would be impossible to guess, if we want the correct exact shape:
F(x,y,z,w) = (...) + z²w² (12(x²+y²-c²)² - 8(a²-b²)(x²-y²) - 8(a²+b²)c² + 4(a²+b²)² - 8(a²-b²)² - 64a²b² + 12(x²+y²-c²)(z²+w²) + 4(a²-b²)(z²-w²) + 4z⁴ + 6z²w² + 4w⁴).
In contrast, my previous approach, of partially expanding the product and adding w² terms where they look like they should fit to match z², only requires further subtracting 64a²b²z²w² at the end to get an exact tiger. But my new approach is much easier for larger n. And we have no way to tell what a "correct" 2n-legged tiger should look like (beyond its general topology); no way to tell what terms should be added at the end, with either approach.
ΓΔΘΛΞΠΣΦΨΩ αβγδεζηθϑικλμνξοπρϱσςτυϕφχψωϖ °±∓½⅓⅔¼¾×÷†‡• ⁰¹²³⁴⁵⁶⁷⁸⁹⁺⁻⁼⁽⁾₀₁₂₃₄₅₆₇₈₉₊₋₌₍₎
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩



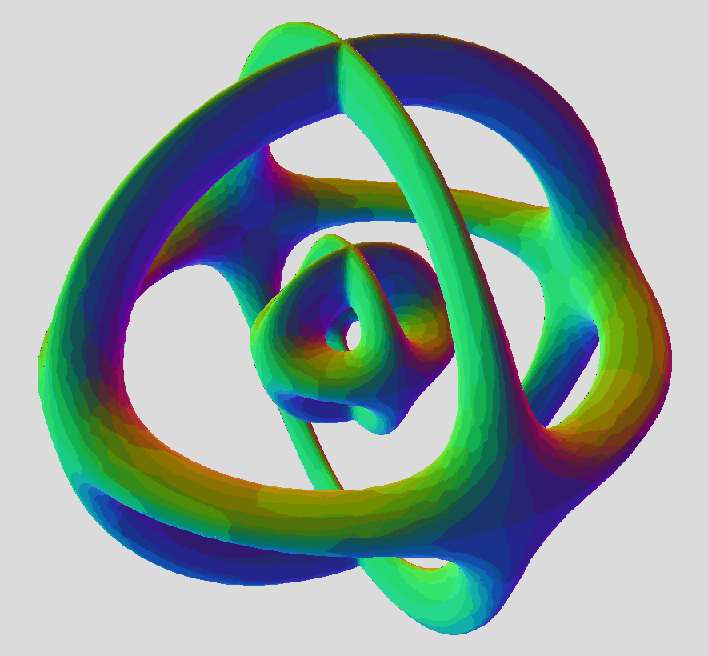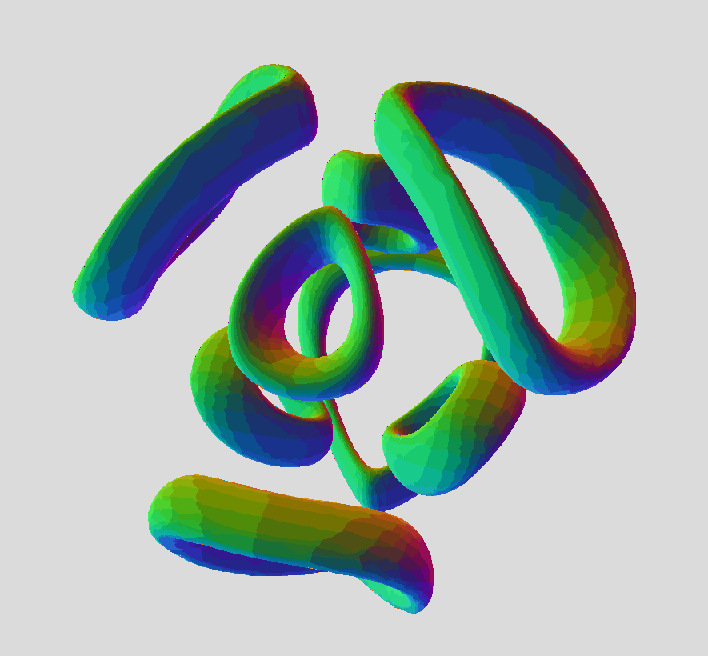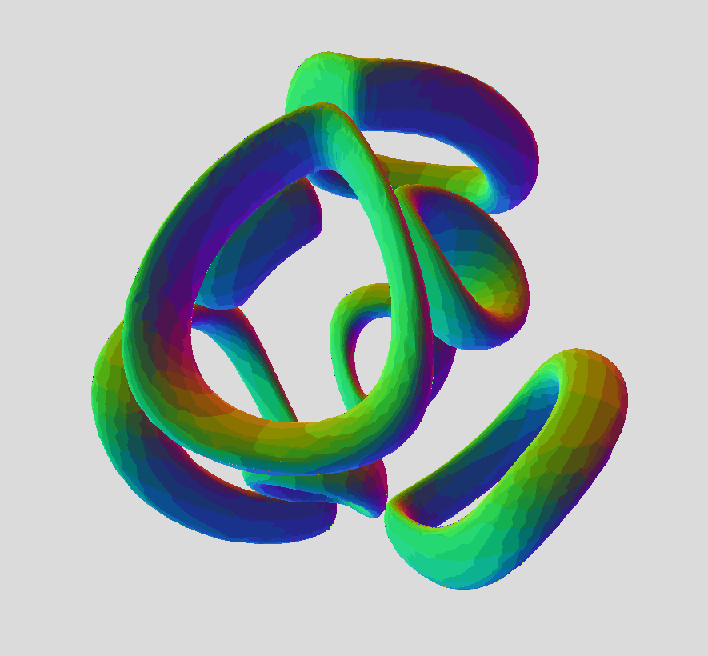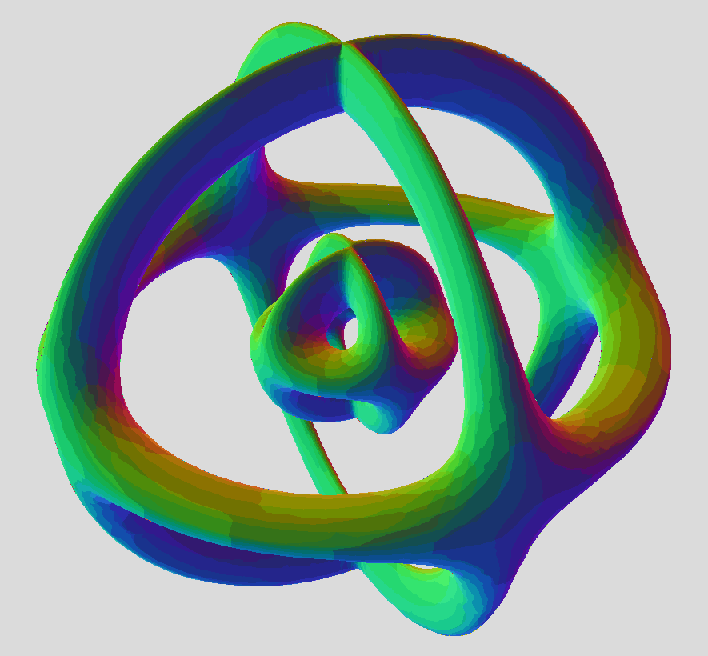

 No need to take a month to expand and simplify the 4-fold product for a spider; just leave the product as is. I'll explain.
No need to take a month to expand and simplify the 4-fold product for a spider; just leave the product as is. I'll explain.


 ) That's not to mention converting 4D to 3D.
) That's not to mention converting 4D to 3D. I mean, I don't know how far I have to go before I can easily convert the 3D polynomial F(x,y,z,0) to the 4D polynomial F(x,y,z,w). And the conversion is not unique; different-looking but equal forms for F(x,y,z,0) may suggest different-looking and unequal forms for F(x,y,z,w). For example (I mentioned this before), I would take b⁶z⁴ and change it to b⁶z⁴+a⁶w⁴, but (b³z²)² I would change to (b³z²+a³w²)² = b⁶z⁴+a⁶w⁴+2a³b³z²w². In any case, we must only add terms involving w (whether inside or outside parentheses), and in such a way that the result has the required symmetries.
I mean, I don't know how far I have to go before I can easily convert the 3D polynomial F(x,y,z,0) to the 4D polynomial F(x,y,z,w). And the conversion is not unique; different-looking but equal forms for F(x,y,z,0) may suggest different-looking and unequal forms for F(x,y,z,w). For example (I mentioned this before), I would take b⁶z⁴ and change it to b⁶z⁴+a⁶w⁴, but (b³z²)² I would change to (b³z²+a³w²)² = b⁶z⁴+a⁶w⁴+2a³b³z²w². In any case, we must only add terms involving w (whether inside or outside parentheses), and in such a way that the result has the required symmetries. I have to admit it. There's no telling how much more research and discoveries I could have made if I were more motivated. My spontaneous interest in things that can end abruptly is my main handicap in life. I'm always chasing the next shiniest object down the next rabbit hole. I don't know of any other existence without it, so I just kinda roll with it now. You know how it goes! Plus, these music video ideas have got me majorly distracted in all areas of my life right now.....
I have to admit it. There's no telling how much more research and discoveries I could have made if I were more motivated. My spontaneous interest in things that can end abruptly is my main handicap in life. I'm always chasing the next shiniest object down the next rabbit hole. I don't know of any other existence without it, so I just kinda roll with it now. You know how it goes! Plus, these music video ideas have got me majorly distracted in all areas of my life right now.....
 (Coincidentally, on the same day, I encountered several large 3D spiders.) I guess it was easier because the coordinate axes are aligned with the spider's symmetry axes. It may be easier in general when n is even, because each torus is exactly opposite another torus, and they can be paired together in the product, which then simplifies according to (u+v)(u-v) = u²-v².
(Coincidentally, on the same day, I encountered several large 3D spiders.) I guess it was easier because the coordinate axes are aligned with the spider's symmetry axes. It may be easier in general when n is even, because each torus is exactly opposite another torus, and they can be paired together in the product, which then simplifies according to (u+v)(u-v) = u²-v². Take a picture of those giant equations you've been scribbling down. I've got to see this.
Take a picture of those giant equations you've been scribbling down. I've got to see this.






