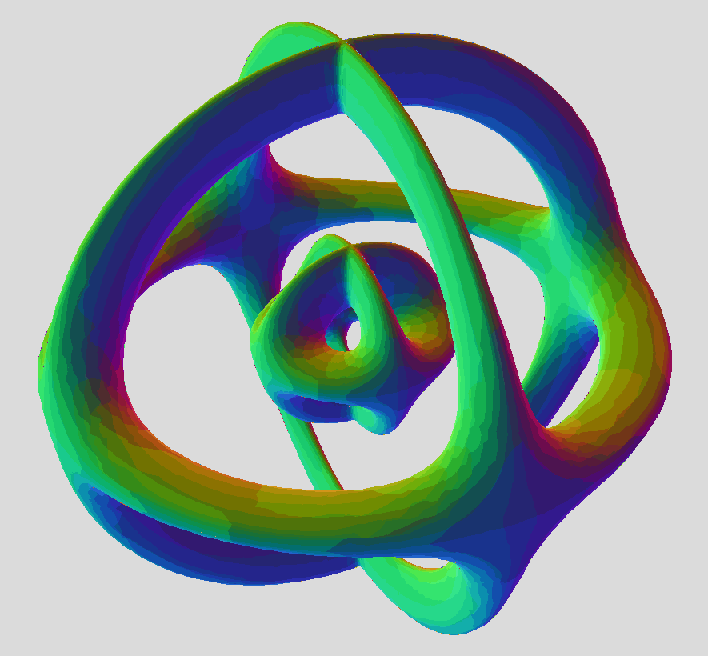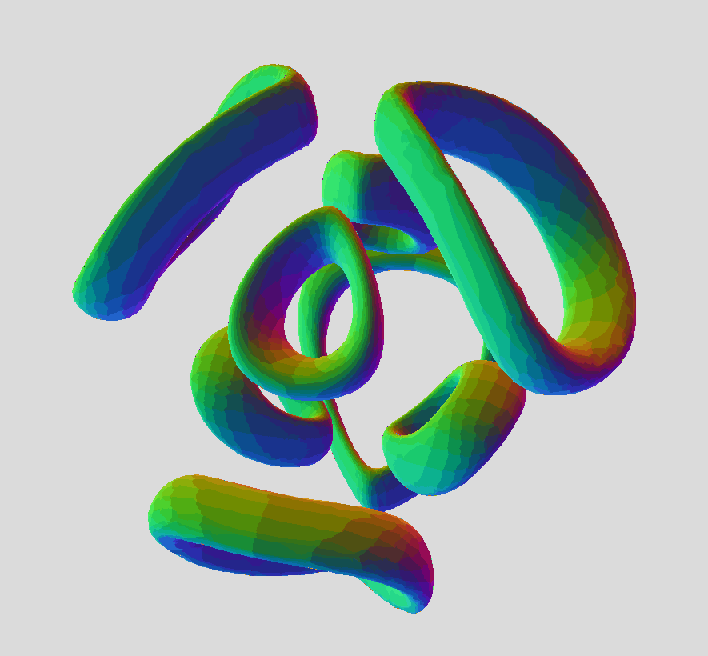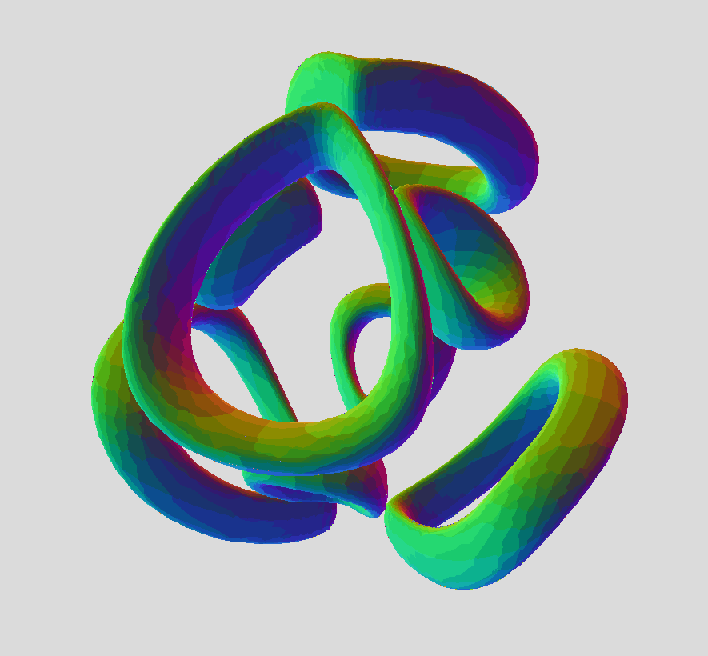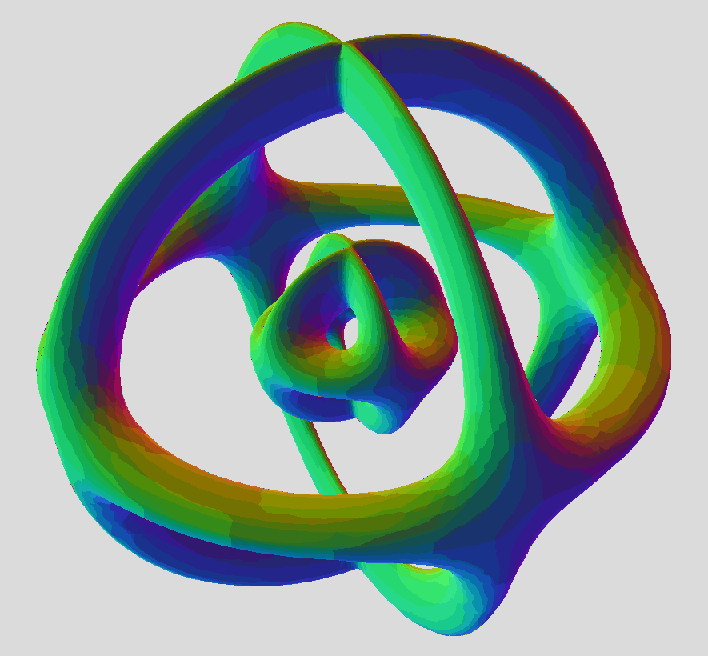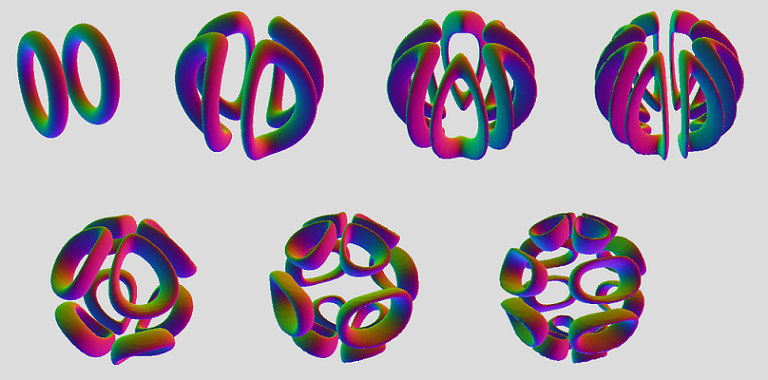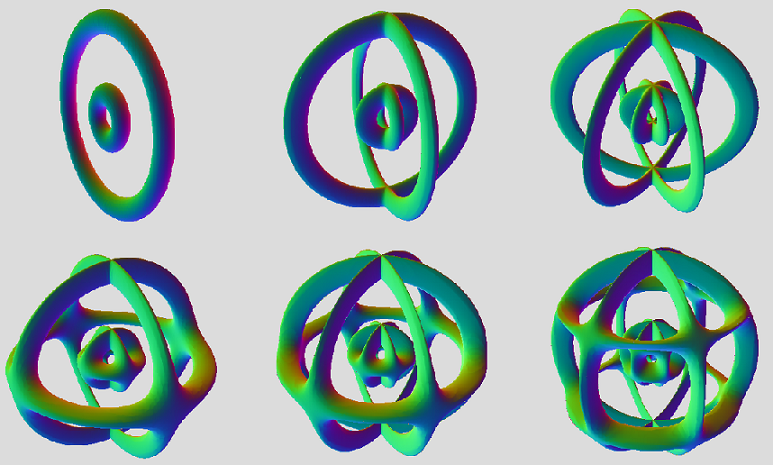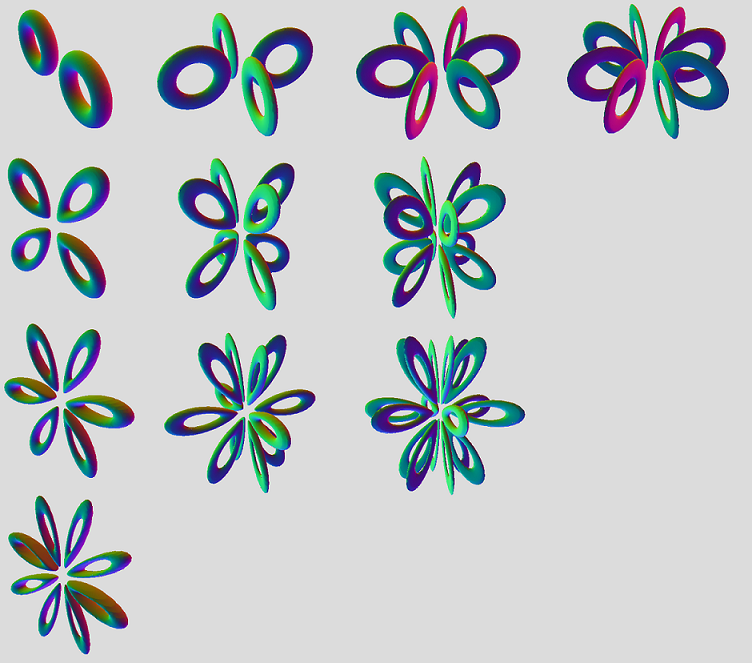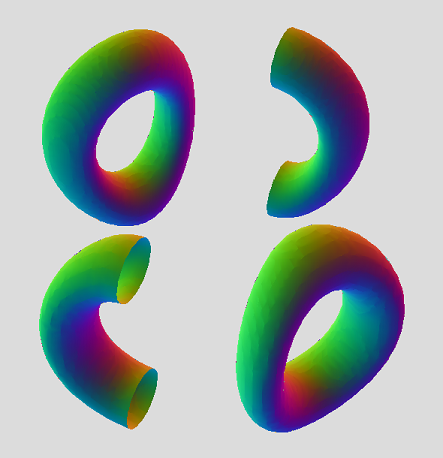All right! I tweaked your mantis skeleton, Marek. Originally, you had
(r^2 * cos(2*fi/3)^2 + y^2 - a^2)^2 + (r^2 * sin(2*fi/3)^2 + w^2 - b^2)^2 = 0
We can transform this back to Cartesian coordinates:
r^2 = x^2 + z^2
fi = arctan(x/z)
((x^2 + z^2) * cos(2*arctan(x/z)/3)^2 + y^2 - a^2)^2 + ((x^2 + z^2) * sin(2*arctan(x/z)/3)^2 + w^2 - b^2)^2 = 0
What I found had worked was,
(sqrt((r*cos(3*fi/2))^2) - a)^2 + (sqrt((r*sin(3*fi/2))^2) - a)^2 = b^2
r = sqrt(x^2 + z^2)
fi = arctan(z/x)
(sqrt(((sqrt(x^2+z^2))*cos(3*(arctan(z/x))/2))^2) - a)^2 + (sqrt(((sqrt(x^2+z^2))*sin(3*(arctan(z/x))/2))^2) - a)^2 = b^2
Makes six ellipses in hexagon

Now, to unite as a midsection in 3D and 4D
Strange structure seen before in 3-intersecting dyad function :
Stack of Genus-2 Tori(sqrt(((sqrt(x^2+z^2))*cos(3*(arctan(z/x))/2))^2 + y^2) - b)^2 + (sqrt(((sqrt(x^2+z^2))*sin(3*(arctan(z/x))/2))^2 + a^2) - b)^2 = d^2

Second midsection: regular tiger cut of column of two tori
(sqrt(((sqrt(x^2+a^2))*cos(3*(arctan(a/x))/2))^2 + y^2) - b)^2 + (sqrt(((sqrt(x^2+a^2))*sin(3*(arctan(a/x))/2))^2 + z^2) - b)^2 = d^2
Third Midsection : tiger cage at 45 degree angle
(sqrt(((sqrt(a^2+x^2))*cos(3*(arctan(x/a))/2))^2 + y^2) - b)^2 + (sqrt(((sqrt(a^2+x^2))*sin(3*(arctan(x/a))/2))^2 + z^2) - b)^2 = d^2
So, it seems to be on the right track, but uniting with presumed 3D and 4D equation, makes two genus-2 tori instead of three genus-1's. Maybe we also need to set up a 3-period rotation for plane YW as well. In 3D, we expect three separate tori, in 2 distinct arrangements. So, we're looking for a degree-12 equation with three periods of a rotated copy of a torus, that share a hexagon array of circles. For tiger, the tori lie flat in XY plane, separated by Z.
This function made two tori in a column, as a cut of tiger, derived by four circles in square array
(sqrt(((sqrt(x^2+z^2))*cos(arctan(z/x)))^2 + y^2) - b)^2 + (sqrt(((sqrt(x^2+z^2))*sin(arctan(z/x)))^2 + a^2) - c)^2 = d^2
Even if we express tiger in duocylindrical coordinates, with a dual 3-period rotation in XZ and YW ( just to experiement):
Tiger in Duocylindrical coordinates:
(sqrt((r1*cos(ϕ1))^2 + (r2*cos(ϕ2))^2) - a)^2 + (sqrt((r1*sin(ϕ1))^2 + (r2*sin(ϕ2))^2) - a)^2 = b^2
Converting to Cartesian
r1 = (sqrt(x^2+z^2))
ϕ1 = (arctan(z/x))
r2 = (sqrt(y^2+w^2))
ϕ2 = (arctan(w/y))
Tigroid with dual 3-period rotation
(sqrt((r1*cos(3*ϕ1/2))^2 + (r2*cos(3*ϕ2/2))^2) - a)^2 + (sqrt((r1*sin(3*ϕ1/2))^2 + (r2*sin(3*ϕ2/2))^2) - a)^2 = b^2
converted
(sqrt(((sqrt(x^2+z^2))*cos(3*(arctan(z/x))/2))^2 + ((sqrt(y^2+w^2))*cos(3*(arctan(w/y))/2))^2) - a)^2 + (sqrt(((sqrt(x^2+z^2))*sin(3*(arctan(z/x))/2))^2 + ((sqrt(y^2+w^2))*sin(3*(arctan(w/y))/2))^2) - a)^2 = b^2
3D midsections
W-cut : same stack of genus-2 tori, as seen in above image
(sqrt(((sqrt(x^2+z^2))*cos(3*(arctan(z/x))/2))^2 + ((sqrt(y^2+a^2))*cos(3*(arctan(a/y))/2))^2) - b)^2 + (sqrt(((sqrt(x^2+z^2))*sin(3*(arctan(z/x))/2))^2 + ((sqrt(y^2+a^2))*sin(3*(arctan(a/y))/2))^2) - b)^2 = d^2
Hmm. I feel like we're getting close here. Need to find how to make a 3-period rotation of a whole torus.