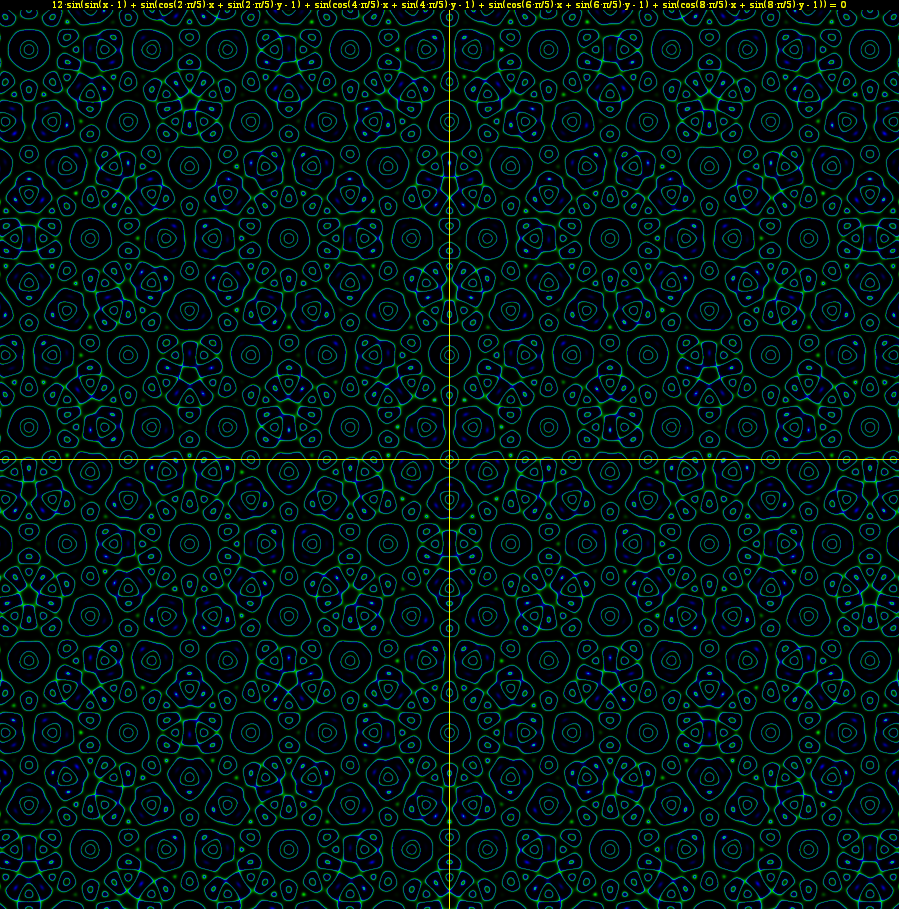
The yellow crosshairs represent the coordinate axes. The region represented by the above image is -120 ≤ x ≤ 120, -120 ≤ y ≤ 120.
In case you can't read the tiny font at the top, the equation is:
- Code: Select all
12·sin(sin(x - 1) +
sin(cos(2·π/5)·x + sin(2·π/5)·y - 1) +
sin(cos(4·π/5)·x + sin(4·π/5)·y - 1) +
sin(cos(6·π/5)·x + sin(6·π/5)·y - 1) +
sin(cos(8·π/5)·x + sin(8·π/5)·y - 1)) = 0
The factor of 12 on the left-hand side is not really necessary; it's just a hack to get my graphing program to show the graph lines more clearly.

The equation looks a bit scary, but it's actually very simple. It can be rewritten simply as:
sin( sum_{i=0 to 4} sin(cos(i*2π/5)*x + sin(i*2π/5)*y - 1) ) = 0
Or, to put it even more simply:
sin( sum( sin( horizontal line rotated by 0°, 72°, 144°, 216°, 288° ) ) ) = 0
The sine function applied to each line basically replicates it into an infinite set of equally-spaced parallel lines. The outer sine function turns the intersections into a series of blob-like pieces that form pretty patterns.
The pentagonal symmetry is a direct result of the orientations of the generating lines. What's interesting, though, is the resulting patterns in the graph. Due to the fact that the coefficients of x and y in pentagonal orientation are irrational, the pattern of intersections between the 5 sets of parallel lines never repeat, so it produces a kaleidoscopic pattern of intersections that are reminiscient of Penrose pentagonal tilings. But what's fascinating is that the outer sine function creates a pattern of blob-like curves in the graph that exhibit all manners of pentagonal, decagonal, and even 20- and 30-fold symmetries, even though if you look more closely, they are actually not perfectly symmetrical except for the patterns centered on the origin. Yet they show almost-pentagonal / almost-decagonal / etc. patterns in a way that suggests some kind of underlying generating principle that one could use to generate Penrose tilings. If you trace the circle-like arrangements of blobs, you'll notice a lot of 5-membered, 10-membered, and 30-membered rings. They aren't actually real, regular pentagons, decagons, 30-gons, they are somewhat distorted but nevertheless they retain their relationship with the central regular pentagonal symmetry.
As the form of the equation suggests, this is only one member of a class of similar equations that I've been exploring. By summing lines rotated across different angles corresponding to subdivisions of the circle, you can get triangular, square, octagonal, etc. patterns. In fact, I have a graph of a heptagonal version of the equation that shows patterns in 14-gonal and 28-gonal symmetries. Truly fascinating!


 I had no idea that there was an actual relation between the two!
I had no idea that there was an actual relation between the two!