Tiger (EntityTopic, 11)
From Hi.gher. Space
m |
m (K6.4 upgrade: img -> embed) |
||
| (14 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| + | <[#ontology [kind topic] [cats 4D Curved Toratope]]> | ||
{{STS Shape | {{STS Shape | ||
| name=Tiger | | name=Tiger | ||
| Line 5: | Line 6: | ||
| genus=1 | | genus=1 | ||
| ssc2=T((2)(2)) | | ssc2=T((2)(2)) | ||
| - | | extra={{STS | + | | extra={{STS Toratope |
| - | | | + | | expand=[[Triocylinder|222]] |
| - | | notation=( | + | | notation=((II)(II)) |
| - | | index= | + | | index=6b |
}}}} | }}}} | ||
| + | |||
| + | The '''tiger''' is the most difficult of the [[four-dimensional torii]] to understand. It was so named because ''tora'', the prefix used for toratopes based on the word ''[[torus]]'', happens to be the Japanese word for tiger, and the name aptly represents that it is a beast to understand. Like its open counterpart, the [[duocylinder]], it has no 3D analog. In 4D, it is possible to have a chain of interlocked tigers which will not come apart, similar to a 3D chain of torii. | ||
== Equations == | == Equations == | ||
| Line 18: | Line 21: | ||
*All points (''x'', ''y'', ''z'', ''w'') that lie on the [[surcell]] of a tiger will satisfy the following equation: | *All points (''x'', ''y'', ''z'', ''w'') that lie on the [[surcell]] of a tiger will satisfy the following equation: | ||
| - | ( | + | <blockquote>(√(''x''<sup>2</sup> + ''y''<sup>2</sup>) − ''a'')<sup>2</sup> + (√(''z''<sup>2</sup> + ''w''<sup>2</sup>) − ''b'')<sup>2</sup> = ''r''<sup>2</sup></blockquote> |
*The [[parametric equations]] are: | *The [[parametric equations]] are: | ||
| - | <blockquote>''x'' = ''a''cos(''θ<sub>1</sub>'') + ''r''cos(''θ<sub>1</sub>'')cos(''θ<sub>3</sub>'')<br> | + | <blockquote>''x'' = ''a'' cos(''θ<sub>1</sub>'') + ''r'' cos(''θ<sub>1</sub>'')cos(''θ<sub>3</sub>'')<br> |
| - | ''y'' = ''a''sin(''θ<sub>1</sub>'') + ''r''sin(''θ<sub>1</sub>'')cos(''θ<sub>3</sub>'')<br> | + | ''y'' = ''a'' sin(''θ<sub>1</sub>'') + ''r'' sin(''θ<sub>1</sub>'')cos(''θ<sub>3</sub>'')<br> |
| - | ''z'' = ''b''cos(''θ<sub>2</sub>'') + ''r''cos(''θ<sub>2</sub>'')sin(''θ<sub>3</sub>'')<br> | + | ''z'' = ''b'' cos(''θ<sub>2</sub>'') + ''r'' cos(''θ<sub>2</sub>'')sin(''θ<sub>3</sub>'')<br> |
| - | ''w'' = ''b''sin(''θ<sub>2</sub>'') + ''r''sin(''θ<sub>2</sub>'')sin(''θ<sub>3</sub>'')</blockquote> | + | ''w'' = ''b'' sin(''θ<sub>2</sub>'') + ''r'' sin(''θ<sub>2</sub>'')sin(''θ<sub>3</sub>'')</blockquote> |
*The [[hypervolume]]s of a tiger are given by: | *The [[hypervolume]]s of a tiger are given by: | ||
| Line 34: | Line 37: | ||
*The [[realmic]] [[cross-section]]s (''n'') of a tiger are: | *The [[realmic]] [[cross-section]]s (''n'') of a tiger are: | ||
<blockquote>For realms parallel to one of the axes, they are formed by rotating Cassini ovals around a line parallel with their major axis, and not intersecting the ovals. </blockquote> | <blockquote>For realms parallel to one of the axes, they are formed by rotating Cassini ovals around a line parallel with their major axis, and not intersecting the ovals. </blockquote> | ||
| + | |||
| + | == Construction == | ||
| + | The tiger could be constructed from a duocylinder similarly to how the torus could be constructed from a cylinder: | ||
| + | <[#embed [hash MGZY4K399MQ5APN1T9QXTKFA7F] [width 900]]><br/> | ||
| + | ''Diagram created by [[Keiji]], adapted from [http://teamikaria.com/hddb/forum/download/file.php?id=63 a sketch] from [[Secret]] in [http://teamikaria.com/hddb/forum/viewtopic.php?p=19287#p19287 this forum post].'' | ||
| + | |||
| + | == Holes == | ||
| + | The tiger has one hole, through which a plane can be inserted in two perpendicular orientations, e.g. ''xy'' and ''zw''. | ||
| + | |||
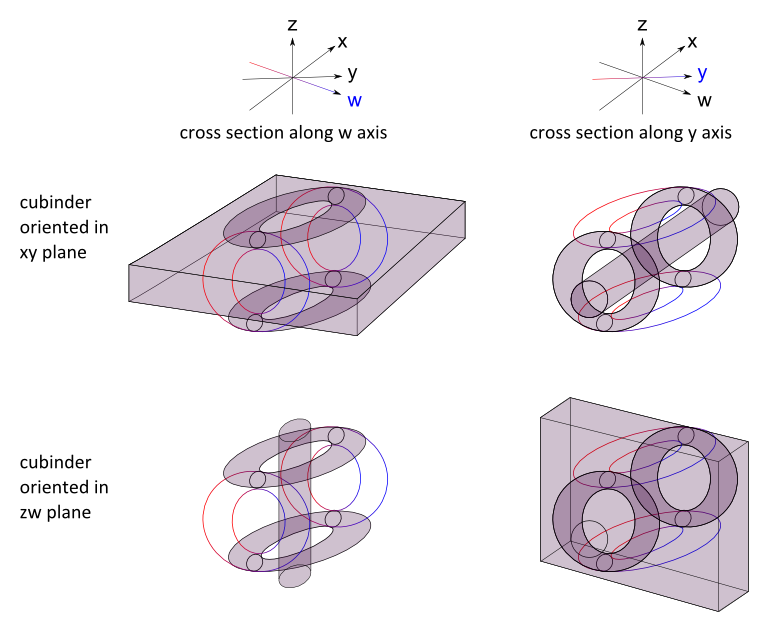
| + | This diagram should help in understanding how the tiger works. In each, a long, thin cubinder is being inserted into the tiger. In the top row, the cubinder is oriented in the ''xy'' plane. In the bottom row, it's oriented in the ''zw'' plane. The tiger is in the same position in all four projections. The red-blue gradiented lines do not appear in the cross-section, but are parts of the tiger which are located in the fourth dimension. | ||
| + | |||
| + | <[#embed [hash V5DVPS9T6S3Y22CSR1DATE2TB7]]> | ||
| + | |||
| + | == Cross-sections == | ||
| + | [[User:Polyhedron Dude|Jonathan Bowers aka Polyhedron Dude]] created these two excellent cross-section renderings:<br/> | ||
| + | <[#embed [hash 0KA30GVG99GPGQ37SXX48BDRXA] [width 676]]><br/> | ||
| + | <[#embed [hash EEWRMK20J64PJM8K47DT05W9V1] [width 676]]> | ||
| + | |||
| + | == External links == | ||
| + | *[http://www.youtube.com/watch?v=fkaI6meNiI0 Rotation animation] | ||
| + | |||
{{Tetrashapes}} | {{Tetrashapes}} | ||
| - | {{ | + | {{Toratope Nav B|5|6|7|(II)II<br>Cubinder|((II)II)<br>Spheritorus|(II)(II)<br>Duocylinder|((II)(II))<br>Tiger|(III)I<br>Spherinder|((III)I)<br>Torisphere|chora}} |
Latest revision as of 20:45, 11 February 2014
The tiger is the most difficult of the four-dimensional torii to understand. It was so named because tora, the prefix used for toratopes based on the word torus, happens to be the Japanese word for tiger, and the name aptly represents that it is a beast to understand. Like its open counterpart, the duocylinder, it has no 3D analog. In 4D, it is possible to have a chain of interlocked tigers which will not come apart, similar to a 3D chain of torii.
Equations
- Variables:
a ⇒ major radius of the tiger in the xy plane
b ⇒ major radius of the tiger in the zw plane
r ⇒ minor radius of the tiger
- All points (x, y, z, w) that lie on the surcell of a tiger will satisfy the following equation:
(√(x2 + y2) − a)2 + (√(z2 + w2) − b)2 = r2
- The parametric equations are:
x = a cos(θ1) + r cos(θ1)cos(θ3)
y = a sin(θ1) + r sin(θ1)cos(θ3)
z = b cos(θ2) + r cos(θ2)sin(θ3)
w = b sin(θ2) + r sin(θ2)sin(θ3)
- The hypervolumes of a tiger are given by:
total edge length = Unknown
total surface area = Unknown
surcell volume = Unknown
bulk = Unknown
- The realmic cross-sections (n) of a tiger are:
For realms parallel to one of the axes, they are formed by rotating Cassini ovals around a line parallel with their major axis, and not intersecting the ovals.
Construction
The tiger could be constructed from a duocylinder similarly to how the torus could be constructed from a cylinder:

Diagram created by Keiji, adapted from a sketch from Secret in this forum post.
Holes
The tiger has one hole, through which a plane can be inserted in two perpendicular orientations, e.g. xy and zw.
This diagram should help in understanding how the tiger works. In each, a long, thin cubinder is being inserted into the tiger. In the top row, the cubinder is oriented in the xy plane. In the bottom row, it's oriented in the zw plane. The tiger is in the same position in all four projections. The red-blue gradiented lines do not appear in the cross-section, but are parts of the tiger which are located in the fourth dimension.
Cross-sections
Jonathan Bowers aka Polyhedron Dude created these two excellent cross-section renderings:


External links
| Notable Tetrashapes | |
| Regular: | pyrochoron • aerochoron • geochoron • xylochoron • hydrochoron • cosmochoron |
| Powertopes: | triangular octagoltriate • square octagoltriate • hexagonal octagoltriate • octagonal octagoltriate |
| Circular: | glome • cubinder • duocylinder • spherinder • sphone • cylindrone • dicone • coninder |
| Torii: | tiger • torisphere • spheritorus • torinder • ditorus |
| 5a. (II)II Cubinder | 5b. ((II)II) Spheritorus | 6a. (II)(II) Duocylinder | 6b. ((II)(II)) Tiger | 7a. (III)I Spherinder | 7b. ((III)I) Torisphere |
| List of toratopes | |||||