I made my first projection animation of a Klein Bottle. Instead of accumulating screenshots and making a gif, I just ran calcplot in realtime and used a screencapture recorder.
https://www.youtube.com/watch?v=aobRi4KQcKA&feature=youtu.be
This animation was made with the parametric equation:
x(u,v) = (3 + sin(v))cos(u)
y(u,v) = (3 + sin(v))sin(u)
z(u,v) = cos(v)cos(u/2)
w(u,v) = cos(v)sin(u/2)
0 < u,v < 2π
rotate on plane xw:
x = (x)*cos(t) + (w)*sin(t)
y = y
z = z
w = (x)*sin(t) - (w)*cos(t)
becomes,
x = ((3 + sin(v))cos(u))*cos(t) + (cos(v)sin(u/2))*sin(t)
y = (3 + sin(v))sin(u)
z = cos(v)cos(u/2)
w = ((3 + sin(v))cos(u))*sin(t) - (cos(v)sin(u/2))*cos(t)
Project on plane xyz:
x(u,v) = ((3 + sin(v))cos(u))*cos(t) + (cos(v)sin(u/2))*sin(t)
y(u,v) = (3 + sin(v))sin(u)
z(u,v) = cos(v)cos(u/2)
w(u,v) = 0
Vary parameter t between 0 and 2π to rotate on plane xw
-----------------
For exploring the cross sections of a mobius tube (klein bottle) , use the implicitized polynomial:
(x^2 +y^2 +z^2 +w^2 -a^2 -b^2)^2 -4a^2(b^2 -z^2 -w^2) = 0
which can also be represented as
(sqrt(x^2 +y^2) -a)^2 +z^2 +w^2 = b^2
rotating on plane xw, set w=d :
x = (x*cos(t) + d*sin(t))
w = (x*sin(t) - d*cos(t))
becomes a movable 3D cross section:
((x*cos(t)+d*sin(t))^2 +y^2 +z^2 +(x*sin(t)-d*cos(t))^2 -a^2 -b^2)^2 -4a^2(b^2 -z^2 -(x*sin(t)-d*cos(t))^2) = 0
set a = 3 ; b = 1
Exploring this function using ‘d’ to translate along w , ’t’ to rotate on xw , you will see all of the slices of a spheritorus:
Rotating at origin : http://i.imgur.com/9AZPAua.mp4
Passing through 3D at various angles : http://i.imgur.com/cYzvzEl.mp4
3D Projection of a Klein Bottle
11 posts
• Page 1 of 1
3D Projection of a Klein Bottle
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: 3D Projection of a Klein Bottle
Here's the yw rotation of the mobius tube. At the pinch, you can see the inversion a little more clearly.
https://www.youtube.com/watch?v=kyACrzsZ3tk&feature=youtu.be
https://www.youtube.com/watch?v=kyACrzsZ3tk&feature=youtu.be
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: 3D Projection of a Klein Bottle
That's a very cool tool ICN5D! I think it would be even more helpful if you were using a perspective projection (even for a rotating 3D object an orthogonal projection can look confusing) and maby color-coding the distance, e.g. like that:


What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 136
- Joined: Wed Jul 29, 2015 1:12 pm
Re: 3D Projection of a Klein Bottle
I'd like to make perspective projections, but I'm not sure how. The wikipedia article is no help. If the parametric equation is:
x(u,v) = (3 + sin(v))cos(u)
y(u,v) = (3 + sin(v))sin(u)
z(u,v) = cos(v)cos(u/2)
w(u,v) = cos(v)sin(u/2)
Orthographic is easy, simply set w=0. What do I need to do for perspective? I use calcplot3D right now, which has 5 adjustable parameters (a,b,c,d,t). I can use these to control the camera distance, which would change the FOV and focal length on the fly.
x(u,v) = (3 + sin(v))cos(u)
y(u,v) = (3 + sin(v))sin(u)
z(u,v) = cos(v)cos(u/2)
w(u,v) = cos(v)sin(u/2)
Orthographic is easy, simply set w=0. What do I need to do for perspective? I use calcplot3D right now, which has 5 adjustable parameters (a,b,c,d,t). I can use these to control the camera distance, which would change the FOV and focal length on the fly.
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: 3D Projection of a Klein Bottle
ICN5D wrote:I'd like to make perspective projections, but I'm not sure how. The wikipedia article is no help. If the parametric equation is:
x(u,v) = (3 + sin(v))cos(u)
y(u,v) = (3 + sin(v))sin(u)
z(u,v) = cos(v)cos(u/2)
w(u,v) = cos(v)sin(u/2)
Orthographic is easy, simply set w=0. What do I need to do for perspective? I use calcplot3D right now, which has 5 adjustable parameters (a,b,c,d,t). I can use these to control the camera distance, which would change the FOV and focal length on the fly.
No worries, it's no big deal.
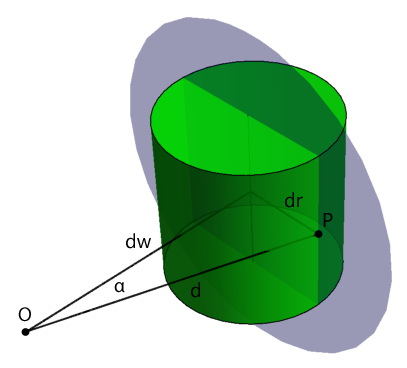
Consider an object (green cylinder) as seen by an observer O. The distance d of a point P of the object has a component parallel to the line of sight along the w-direction dw and a component perpendicular to the line of sight dr. When you do an orthogonal projection of a point P, you just set its distance from the center of the image equal to dr = sqrt(x²+y²+z²) in the object. For an observer O, however, the distance P appears from the center of the image is given by the angle alpha to the line of sight. alpha is given by arctan(dr/dw) = arctan(sqrt(x²+y²+z²)/(w+w0)). x, y, z and w are the coordinates of the coordinate system of the object, w0 is the distance of the object's center from O. In total the image of of a point (x, y, z, w) is the product of the angle alpha and the normalized vector perpendicular to the line of sight (x, y, z)/sqrt(x²+y²+z²)
Proj(x, y, z, w) = arctan[sqrt(x²+y²+z²)/(w+w0)]/sqrt(x²+y²+z²)*(x, y, z)
This is rather lengthy and arctan is a nasty function, but for small angles, as you typically see smaller everyday objects, alpha is a good approximation for arctan(alpha). As a consequency the square roots cancel each other and the expression becomes much more economic. The perspective projection of a point is then approximately
Proj(x, y, z, w) =~ (x, y, z)/(w+w0)
In order to keep the error below 2%, w0 should be at least four times larger than the maximum radius (sqrt(x²+y²+z²)) of the object. If you want to fix w0, I wouldn't make it much larger than that, as the perspective effect gets smaller and smaller with the distance.
PS.: If you want to get really close to objects and you have enough computing power, you could take also into account the third order term of arctan(alpha) ~= alpha - alpha³/3, and use Proj(x, y, z, w) =~ (x, y, z)*[1/(w+w0) - (x²+y²+z²)/(3(w+w0)³)]. The error for rmax/w0 = 1/2 is then around 1%.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 136
- Joined: Wed Jul 29, 2015 1:12 pm
Re: 3D Projection of a Klein Bottle
Oh, cool. This is interesting! I'm still not sure how to change the parametric equation into what it needs to be. How do I use
Proj(x, y, z, w) =~ (x, y, z)/(w+w0)
with.
x = (3 + sin(v))cos(u)
y = (3 + sin(v))sin(u)
z = cos(v)cos(u/2)
w = cos(v)sin(u/2)
?
Is it something like (where, w0 = 7) ...
x = ((3 + sin(v))cos(u))/(cos(v)sin(u/2) + 7)
y = ((3 + sin(v))sin(u))/(cos(v)sin(u/2) + 7)
z = (cos(v)cos(u/2))/(cos(v)sin(u/2) + 7)
?
Proj(x, y, z, w) =~ (x, y, z)/(w+w0)
with.
x = (3 + sin(v))cos(u)
y = (3 + sin(v))sin(u)
z = cos(v)cos(u/2)
w = cos(v)sin(u/2)
?
Is it something like (where, w0 = 7) ...
x = ((3 + sin(v))cos(u))/(cos(v)sin(u/2) + 7)
y = ((3 + sin(v))sin(u))/(cos(v)sin(u/2) + 7)
z = (cos(v)cos(u/2))/(cos(v)sin(u/2) + 7)
?
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: 3D Projection of a Klein Bottle
Exactly.
But you should choose a larger w0. rmax is 4 in your case (e.g. plug in v = pi/2 and u = 0), so rmax/w0 = 4/7 and the distortion is about 23%. I've figured out that part of the distortion is just making the object look closer than it is, so instead of 7 the appearant distance is 6.5. The "real" distortion is only 8%. Anyway w0 >= 10 (w0 >= 2.5*rmax) seems to be a reasonable limit if you are using this formula (real distortion 3.3%).
But you should choose a larger w0. rmax is 4 in your case (e.g. plug in v = pi/2 and u = 0), so rmax/w0 = 4/7 and the distortion is about 23%. I've figured out that part of the distortion is just making the object look closer than it is, so instead of 7 the appearant distance is 6.5. The "real" distortion is only 8%. Anyway w0 >= 10 (w0 >= 2.5*rmax) seems to be a reasonable limit if you are using this formula (real distortion 3.3%).
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 136
- Joined: Wed Jul 29, 2015 1:12 pm
Re: 3D Projection of a Klein Bottle
Well, I tried out the perspective projection equation, and it works amazingly well! I found that w0 = 5 is a good camera distance for reasonable distortion. This is terrific, thank you for that. I've been trying to figure this out for a while.
Today I checked out the mobius tube with rotation on plane xw, yw, and a combined rotate function of planes xy and yw. I also had a look at a flat 2-torus. Being able to see the 4D distance of these surfaces is really amazing.
Do you know anything about making a cross section of a parametric equation, algebraically? Say I had a torus with equation:
x = (cos(u)+2)cos(v)
y = (cos(u)+2)sin(v)
z = sin(u)
How would I algebraically modify the equation to make a 2D slice? If this were an implicit equation, I'd just set any single variable to 0 (x or z), or some adjustable parameter. Parametric needs a different technique.
Today I checked out the mobius tube with rotation on plane xw, yw, and a combined rotate function of planes xy and yw. I also had a look at a flat 2-torus. Being able to see the 4D distance of these surfaces is really amazing.
Do you know anything about making a cross section of a parametric equation, algebraically? Say I had a torus with equation:
x = (cos(u)+2)cos(v)
y = (cos(u)+2)sin(v)
z = sin(u)
How would I algebraically modify the equation to make a 2D slice? If this were an implicit equation, I'd just set any single variable to 0 (x or z), or some adjustable parameter. Parametric needs a different technique.
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: 3D Projection of a Klein Bottle
ICN5D wrote: How would I algebraically modify the equation to make a 2D slice? If this were an implicit equation, I'd just set any single variable to 0 (x or z), or some adjustable parameter. Parametric needs a different technique.
No, it's exactly the same! But you can't just ignore the function that x was before; otherwise the equations will not be satisfied, and you're no longer on the surface.
x = (cos u + 2) cos v
y = (cos u + 2) sin v
z = sin u
0 = (cos u + 2) cos v
0 = (cos u + 2), or 0 = cos v
The cosine function is bounded by 1 and -1, so the first equation is impossible. Thus
cos v = 0
sin v = +/- 1
y = (cos u + 2) (sin v) = +/- (2 + cos u)
z = sin u
These are the modified equations for a cross-section. There's only one variable u, as expected for a pair of circles. Actually, it's only one circle for a given value of v; the two circles are from the +/- sign.
---
More interesting problem, the tiger:
x = (a+c cos t) cos u
y = (a+c cos t) sin u
z = (b+c sin t) cos v
w = (b+c sin t) sin v
Let's intersect this with the hyperplane x = d :
(a+c cos t) cos u = d
cos t = d/c sec u - a/c
sin t = +/- sqrt{1 - (cos t)^2} = +/- sqrt{1 - (d/c sec u)^2 + 2(ad sec u)/c^2 - (a/c)^2}
Plug these sin t and cos t into the original equations, and we've eliminated the variable t, so y,z,w are functions of u,v. (We could have eliminated u instead, and left t,v.)
- mr_e_man
- Tetronian
- Posts: 489
- Joined: Tue Sep 18, 2018 4:10 am
Re: 3D Projection of a Klein Bottle
Or, instead of trying to solve complicated equations to reduce the number of parameters...
Could you use transparency instead of colouring to show distance? Then the points closer to the chosen hyperplane would be more visible, and the points far away would be invisible. That should have almost the same effect as a cross-section, while being smooth and continuous instead of a sharp cut.
Could you use transparency instead of colouring to show distance? Then the points closer to the chosen hyperplane would be more visible, and the points far away would be invisible. That should have almost the same effect as a cross-section, while being smooth and continuous instead of a sharp cut.
ΓΔΘΛΞΠΣΦΨΩ αβγδεζηθϑικλμνξοπρϱσςτυϕφχψωϖ °±∓½⅓⅔¼¾×÷†‡• ⁰¹²³⁴⁵⁶⁷⁸⁹⁺⁻⁼⁽⁾₀₁₂₃₄₅₆₇₈₉₊₋₌₍₎
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
- mr_e_man
- Tetronian
- Posts: 489
- Joined: Tue Sep 18, 2018 4:10 am
Re: 3D Projection of a Klein Bottle
Well, thanks for this! I actually figured out a way to do this a while back, and detailed it here:
Quora answer
It involved some tricky manipulations that weren't clear to me, but I knew there had to be a way, lol. Perseverance always wins!
Quora answer
It involved some tricky manipulations that weren't clear to me, but I knew there had to be a way, lol. Perseverance always wins!
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
11 posts
• Page 1 of 1
Who is online
Users browsing this forum: No registered users and 15 guests
