Particle Spin in 4d
28 posts
• Page 1 of 1
Particle Spin in 4d
In our Universe one of the fundamental properties of particles is their spin. In 3d it's only possible for a spinning object to have one independent direction of spin but in 4d it's possible for a spinning object to have two independent directions of spin. I was wondering would the fact that things can have a double rotation in 4d effect the fundamental spin of the fundamental particles?
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
- anderscolingustafson
- Tetronian
- Posts: 316
- Joined: Mon Mar 22, 2010 6:39 pm
Re: Particle Spin in 4d
Rotations in 4D have some unusual characteristics not present in 3D.
The most prominent is the Clifford isoclinic rotation, in which the two orthogonal rotations proceed at an equal rate. When the two rotation rates are not equal, some points in the object will trace out spirals whereas those that lie on one of the stationary planes of the other rotation will trace out circles. So there are two distinguished stationary planes, orthogonal to each other, where points on the object will trace out circles. Outside of these two planes, points on the object will follow a non-circular spiralling path. However, in the isoclinic rotation, all points of the object trace out circles, and each of these circles lie in a stationary plane! So then there is an infinite number of stationary planes, and the original two orthogonal planes of rotation become indistinguishible from all the other stationary planes. The rotation therefore loses its distinctness in orientation: you could have started out with any orthogonal pair of rotations that lie in any corresponding pair of these infinite number of planes, and you'll get an identical rotation. So a whole bunch of rotations that would have been distinct, if the two rotation rates were different, have collapsed into a single isoclinic rotation.
However, this doesn't mean the rotation is completely independent of orientation! In fact, there are still an infinite number of distinct isoclinic rotations. They are produced if you rotate the planes of rotation along a direction that doesn't lie in any of its stationary planes. Furthermore, the isoclinic rotation is chiral -- there are two distinct "senses" of rotation given the same (infinite) set of stationary planes, and they cannot be reoriented into each other using only rigid motion. They are mirror images of each other.
Now, Wendy has mentioned before that any object that begins with two unequal rates of rotation will eventually settle into an isoclinic rotation via energy transfer -- because there is a gradient of different momentums in different parts of the object, that will prefer to equalize over time in order to reduce the total potential energy. So given any object in its natural state, it will basically always be found in an isoclinic rotation, rather than having two unequal rates of rotation. This suggests that 4D particles would be found with isoclinic spin in their ground state.
The interesting thing about this, is that the chirality of isoclinic rotations means that there are two possible such ground states, corresponding with the two possible chiralities of the isoclinic spin! So this seems to suggest an inherent two-charge or two-spin system, that arises purely from geometry alone!
The most prominent is the Clifford isoclinic rotation, in which the two orthogonal rotations proceed at an equal rate. When the two rotation rates are not equal, some points in the object will trace out spirals whereas those that lie on one of the stationary planes of the other rotation will trace out circles. So there are two distinguished stationary planes, orthogonal to each other, where points on the object will trace out circles. Outside of these two planes, points on the object will follow a non-circular spiralling path. However, in the isoclinic rotation, all points of the object trace out circles, and each of these circles lie in a stationary plane! So then there is an infinite number of stationary planes, and the original two orthogonal planes of rotation become indistinguishible from all the other stationary planes. The rotation therefore loses its distinctness in orientation: you could have started out with any orthogonal pair of rotations that lie in any corresponding pair of these infinite number of planes, and you'll get an identical rotation. So a whole bunch of rotations that would have been distinct, if the two rotation rates were different, have collapsed into a single isoclinic rotation.
However, this doesn't mean the rotation is completely independent of orientation! In fact, there are still an infinite number of distinct isoclinic rotations. They are produced if you rotate the planes of rotation along a direction that doesn't lie in any of its stationary planes. Furthermore, the isoclinic rotation is chiral -- there are two distinct "senses" of rotation given the same (infinite) set of stationary planes, and they cannot be reoriented into each other using only rigid motion. They are mirror images of each other.
Now, Wendy has mentioned before that any object that begins with two unequal rates of rotation will eventually settle into an isoclinic rotation via energy transfer -- because there is a gradient of different momentums in different parts of the object, that will prefer to equalize over time in order to reduce the total potential energy. So given any object in its natural state, it will basically always be found in an isoclinic rotation, rather than having two unequal rates of rotation. This suggests that 4D particles would be found with isoclinic spin in their ground state.
The interesting thing about this, is that the chirality of isoclinic rotations means that there are two possible such ground states, corresponding with the two possible chiralities of the isoclinic spin! So this seems to suggest an inherent two-charge or two-spin system, that arises purely from geometry alone!
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Particle Spin in 4d
And this furthermore leads back to the electromagnetic field through a bar magnet. I mentioned before about the possible duocylinder shaped magnetic field. Have you found anything new on the subject? With respect to the Hopf fibration, and its application to the flow of the EM field through a bar magnet? This isoclinic spin generating a two-charge system, and the duocylinder as an artifact of the Hopf fibration. Seems to be some connection can be made, right?



It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: Particle Spin in 4d
Probably some connection can be made. But no, I haven't had the time to think about this... too busy with RL things. 
But that animation of the tesseract you have is lackluster... it's only showing a single rotation! Here's a more mindblowing one from my website (shameless plug):

This animation shows the 16 truncated tetrahedra in the runcitruncated 16-cell undergoing an isoclinic double rotation. The other cells are not shown, for clarity's sake. Being derived from tesseractic symmetry, these truncated tetrahedra correspond directly to the vertices of the tesseract, or, equivalently, to the tetrahedra of the 16-cell (the "hyperoctahedron", aka the dual of the tesseract). If you follow the cells carefully you can see how they trace out circles in oblique planes -- these are a subset of the infinite number of stationary planes in an isoclinic rotation.

But that animation of the tesseract you have is lackluster... it's only showing a single rotation! Here's a more mindblowing one from my website (shameless plug):


This animation shows the 16 truncated tetrahedra in the runcitruncated 16-cell undergoing an isoclinic double rotation. The other cells are not shown, for clarity's sake. Being derived from tesseractic symmetry, these truncated tetrahedra correspond directly to the vertices of the tesseract, or, equivalently, to the tetrahedra of the 16-cell (the "hyperoctahedron", aka the dual of the tesseract). If you follow the cells carefully you can see how they trace out circles in oblique planes -- these are a subset of the infinite number of stationary planes in an isoclinic rotation.
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Particle Spin in 4d
The notion of 'spin' is fairly recent (some time this century), and i don't necessarily completely understand it. But it is supposed to be attached to the notion of a rotating particle. For an electron, a 'spin-half' particle, means it assumes the same state after having rotated by 720 degrees. Half-spin particles obey the Fermi Dirac statistics and thus called 'fermions', while integer-spin follow the 'bose-einstein' statistics, are called 'bosons'. The essential difference is that no two fermions can have the same description: any orbital can only be occupied by exactly two electrons, one 'spin-up' the other 'spin-down'. This is the Pauli Exclusion principle.
A free particle in 4D would, by transfer of energy between modes, tend to assume a clifford-rotation. Clifford-rotations have a parity (ie left and right), which are mirror-images of each other. But even among the left-handed rotations, there is a separate rotation for each point on the sphere. The twelftychoron has rings of ten decagons on its surface. There are seventy-two such rings, and because each can be transversed either direction, 144 great arrows of order ten. A set of left-clifford rotations divides this 144 into 12 sets of 12. These 12 sets are represented on the sphere as the vertices of an icosahedron. There is another set of 12*12 representing the 12 right-hand rotations.
So if you are looking at a particle, and at its surface, the points near a ring tend to travel as the fingers of the right hand, when the thumb is pointing in the direction of rotation, then it's a right-hand rotation.
Even something like the rotation of planets brings to us, that just as in 3d, we have time-zones on earth, on 4d, there are season-zones, then the nature of spin is something to be holden.
For example, spin might be represented by quarterion multiplication, which follows clifford-rotations, and the interaction of particles might be assymetric (ie ab <> ba), and dependent on things we are not mindful of. This means that one could combine two spinning particles at different states, and produce an outwards particles of different spinning states.
Note that if this were true, and a left and right particle interracted, the outcome would be a wheel-rotation (ie the orthogonal as zero), and some kind of radiation needed to come in or out, to produce a clifford rotation.
A free particle in 4D would, by transfer of energy between modes, tend to assume a clifford-rotation. Clifford-rotations have a parity (ie left and right), which are mirror-images of each other. But even among the left-handed rotations, there is a separate rotation for each point on the sphere. The twelftychoron has rings of ten decagons on its surface. There are seventy-two such rings, and because each can be transversed either direction, 144 great arrows of order ten. A set of left-clifford rotations divides this 144 into 12 sets of 12. These 12 sets are represented on the sphere as the vertices of an icosahedron. There is another set of 12*12 representing the 12 right-hand rotations.
So if you are looking at a particle, and at its surface, the points near a ring tend to travel as the fingers of the right hand, when the thumb is pointing in the direction of rotation, then it's a right-hand rotation.
Even something like the rotation of planets brings to us, that just as in 3d, we have time-zones on earth, on 4d, there are season-zones, then the nature of spin is something to be holden.
For example, spin might be represented by quarterion multiplication, which follows clifford-rotations, and the interaction of particles might be assymetric (ie ab <> ba), and dependent on things we are not mindful of. This means that one could combine two spinning particles at different states, and produce an outwards particles of different spinning states.
Note that if this were true, and a left and right particle interracted, the outcome would be a wheel-rotation (ie the orthogonal as zero), and some kind of radiation needed to come in or out, to produce a clifford rotation.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2014
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Particle Spin in 4d
That's an awesome render, quickfur! Yes, it blows the tesseract away by coolness factor.
Wow, very fascinating! Every time I imagine something like that, I go to high-D thinking. Take the shape of electron orbitals, they're all over the place in symmetrical clumps of possibility. Those multiple locations for an electron of the same energy reminds me of multiple interceptions in our 3D plane. Surely some high-D stuff is going on there! I imagine all atoms stretched along space-time would look like helices entangling with other helices, in cycles of cycles of cycles. As the universe cools, the helices tangle into larger systems, governed by new laws, while composed of the initial helical soup.
wendy wrote:The notion of 'spin' is fairly recent (some time this century), and i don't necessarily completely understand it. But it is supposed to be attached to the notion of a rotating particle. For an electron, a 'spin-half' particle, means it assumes the same state after having rotated by 720 degrees. Half-spin particles obey the Fermi Dirac statistics and thus called 'fermions', while integer-spin follow the 'bose-einstein' statistics, are called 'bosons'. The essential difference is that no two fermions can have the same description: any orbital can only be occupied by exactly two electrons, one 'spin-up' the other 'spin-down'. This is the Pauli Exclusion principle.
A free particle in 4D would, by transfer of energy between modes, tend to assume a clifford-rotation. Clifford-rotations have a parity (ie left and right), which are mirror-images of each other. But even among the left-handed rotations, there is a separate rotation for each point on the sphere. The twelftychoron has rings of ten decagons on its surface. There are seventy-two such rings, and because each can be transversed either direction, 144 great arrows of order ten. A set of left-clifford rotations divides this 144 into 12 sets of 12. These 12 sets are represented on the sphere as the vertices of an icosahedron. There is another set of 12*12 representing the 12 right-hand rotations.
Wow, very fascinating! Every time I imagine something like that, I go to high-D thinking. Take the shape of electron orbitals, they're all over the place in symmetrical clumps of possibility. Those multiple locations for an electron of the same energy reminds me of multiple interceptions in our 3D plane. Surely some high-D stuff is going on there! I imagine all atoms stretched along space-time would look like helices entangling with other helices, in cycles of cycles of cycles. As the universe cools, the helices tangle into larger systems, governed by new laws, while composed of the initial helical soup.
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: Particle Spin in 4d
ICN5D wrote:That's an awesome render, quickfur! Yes, it blows the tesseract away by coolness factor.
There are even cooler ones yet.
 For example, this one is a cross-eyed stereogram animation:
For example, this one is a cross-eyed stereogram animation:
This is the runcitruncated tesseract undergoing isoclinic rotation. I could stare at these things all day, had I the time...

[...]
Wow, very fascinating! Every time I imagine something like that, I go to high-D thinking. Take the shape of electron orbitals, they're all over the place in symmetrical clumps of possibility. Those multiple locations for an electron of the same energy reminds me of multiple interceptions in our 3D plane. Surely some high-D stuff is going on there!
In fact, there is higher dimensional stuff going on with the orbitals -- those strange lobe shapes of orbitals are actually intersections of 6D standing waveforms with 3D space... However, the 6D here isn't your usual 6D, because it's actually 3D complex space (i.e., 3D space where coordinates are complex numbers). What you see as orbital shapes is actually just the 3 real components of the 6D vectors consisting of 3 real components and 3 "imaginary" components. So the electrons are actually standing waves in complex space, and their real components (IOW intersection with "real" 3D space) are what gives the orbitals their shape.
There's some pretty deep stuff going on with these waves in complex space. I recently read an article that suggests that even though in electromagnetism we generally compute voltages, currents, etc., with complex numbers, and simply discard the imaginary component at the end (to get an actual measurable value that can be verified by experiment), electrons and other charged particles actually "feel" the (unmeasurable) imaginary component of an electric charge as well! There have been some experiments that suggest that charged particles behave differently when interacting with another charge that has a different complex component, even if the real components are equal.
I imagine all atoms stretched along space-time would look like helices entangling with other helices, in cycles of cycles of cycles. As the universe cools, the helices tangle into larger systems, governed by new laws, while composed of the initial helical soup.
It's actually not helices, but standing waves. So imagine if you will, a 6D sphere, in which there's a standing wave. The waveform will have a radial component, basically showing up as concentric spheres, and a transverse component, showing up as nodal (hyper)planes passing through the center (analogous to node lines in 2D standing waves, such as those found on the surface of a drum). What we see in 3D is just a slice through this standing wave pattern. The two lobes of a p-orbital, for example, are actually not teardrop-shaped with a long sharp tail, as commonly depicted; a more accurate depiction of them is two halves of a sphere, with a nodal plane between them, IOW, hemispherical in shape.
The most interesting case occurs with the d orbitals: they are often depicted as quartets of teardrop-shaped lobes, but actually this isn't accurate. Fundamentally, they are spheres divided by two perpendicular nodal planes into 4 quarters. The most interesting thing, though, is the occurrence of a 5th shape, commonly depicted as a pair of teardrop shapes girded by a torus ring. Again, this isn't altogether accurate; it's actually a sphere where there are two cone-shaped nodal 2-manifolds that slice through it, cutting it into an upper and lower lobe (more teardrop-like in shape, as oft depicted!) and an equatorial slice that wraps around the origin. This funny-looking shape is actually present in all the d orbitals, except that in the other 4 configurations they lie only in the imaginary components, so they are not seen from "real" 3D space! The 4-lobe shape is actually also present in the "ringed" d-orbital -- if you slice the orbital in half, you'll get what amounts to a circle sliced into 4 quarters by a pair of diagonal node lines. This is the same slice you'd get with the other d orbitals too, except here, one of the other dimensions of the 4-fold lobe lies in imaginary space, while its circular component lies in real space, so we see the ring shape instead of the 4-lobe shape. Conversely, the 4-lobe shape of the other d orbitals are actually slices of 6D rings, so what looks like 4 lobes to us, is actually a pair of annular ring-like shapes in 6D.
 We only see them as 4 lobes because 3D real space intersects with them perpendicularly.
We only see them as 4 lobes because 3D real space intersects with them perpendicularly.- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Particle Spin in 4d
Is this an accurate representation of them?
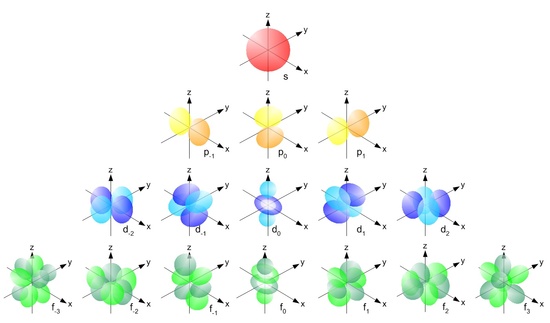
I am familiar with the use of complex numbers in electrical engineering. I didn't expect it to translate over to electron orbitals, though it makes sense. It seems to be unavoidable when describing anything electron. But, those complex dimensions are fascinating! I can't wrap my mind around how that works, other than to assume it's just regular space, but in some funny configuration unlike anything I've heard about. Also intriguing is the notion that electrons still feel the complex component, given the same real component. This seems like the complex space is still real, but hidden in a mysterious way as if above our 3-plane, joined to what we observe to be the real component.
I remember learning way back how to represent a parabola with complex roots, as in no x-intercepts. It can be graphed in a 3D coordinate plane, with Z as the depth of complex space. The parabola would end up being a 2D object that is displaced into Z, parallel to XY.
So, I guess this 3D complex manifold is much like this concept, where the orbitals are in fact real, but suspended above the "real-number" 3D manifold, and never becoming part of what we actually see. But, still very much a physical part whose existence cannot be denied.

I am familiar with the use of complex numbers in electrical engineering. I didn't expect it to translate over to electron orbitals, though it makes sense. It seems to be unavoidable when describing anything electron. But, those complex dimensions are fascinating! I can't wrap my mind around how that works, other than to assume it's just regular space, but in some funny configuration unlike anything I've heard about. Also intriguing is the notion that electrons still feel the complex component, given the same real component. This seems like the complex space is still real, but hidden in a mysterious way as if above our 3-plane, joined to what we observe to be the real component.
I remember learning way back how to represent a parabola with complex roots, as in no x-intercepts. It can be graphed in a 3D coordinate plane, with Z as the depth of complex space. The parabola would end up being a 2D object that is displaced into Z, parallel to XY.
So, I guess this 3D complex manifold is much like this concept, where the orbitals are in fact real, but suspended above the "real-number" 3D manifold, and never becoming part of what we actually see. But, still very much a physical part whose existence cannot be denied.
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: Particle Spin in 4d
That diagram is certainly more accurate than tear-drop shaped orbital depictions (often employed in VSEPR theory).  Nevertheless, the p orbitals are not ellipsoidal, as depicted here. They are more like dumbbell shapes. So this diagram probably still represents an artist's vision of the orbitals, rather than a mathematically accurate depiction.
Nevertheless, the p orbitals are not ellipsoidal, as depicted here. They are more like dumbbell shapes. So this diagram probably still represents an artist's vision of the orbitals, rather than a mathematically accurate depiction. 
In any case, the "true" orbitals are actually mathematically infinite in extent, though their probability density drops exponentially with distance. So it's really a judgment call to decide where to cut off the probability wave pattern and say "here's the boundary of the orbital". Actually, orbitals don't have sharp boundaries. They are probably more accurately understood as "electron clouds" with a particular shape, but the boundary of this cloud is fuzzy.
In any case, the orbital shapes that we see are basically the intersections of the real 3D hyperplane with the "full" orbital shapes in complex 3D space (i.e., 6D space, in effect).
 Nevertheless, the p orbitals are not ellipsoidal, as depicted here. They are more like dumbbell shapes. So this diagram probably still represents an artist's vision of the orbitals, rather than a mathematically accurate depiction.
Nevertheless, the p orbitals are not ellipsoidal, as depicted here. They are more like dumbbell shapes. So this diagram probably still represents an artist's vision of the orbitals, rather than a mathematically accurate depiction. 
In any case, the "true" orbitals are actually mathematically infinite in extent, though their probability density drops exponentially with distance. So it's really a judgment call to decide where to cut off the probability wave pattern and say "here's the boundary of the orbital". Actually, orbitals don't have sharp boundaries. They are probably more accurately understood as "electron clouds" with a particular shape, but the boundary of this cloud is fuzzy.
In any case, the orbital shapes that we see are basically the intersections of the real 3D hyperplane with the "full" orbital shapes in complex 3D space (i.e., 6D space, in effect).
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Particle Spin in 4d
http://www.chm.davidson.edu/vce/atomicorbitals/d-orbitals.html
It seems it is more than that for some orbitals
e.g.
Some of the d orbitals are actually a superposition of 2 of them since they lie entirely in the complex space
I have trouble finding the wavefunctions of d orbitals to check out their original glory. Anyone manage to find them?
It seems it is more than that for some orbitals
The d orbital with m = 0 is designated z2. The two orbitals created from the m = -1 and +1 orbitals are designated xz and yz. The two orbitals created from the m = -2 and +2 orbitals are designated xy and x2-y2. These designations arise from the mathematical formulas for the wave functions and indicate the orientation of the orbital.
e.g.
Some of the d orbitals are actually a superposition of 2 of them since they lie entirely in the complex space
I have trouble finding the wavefunctions of d orbitals to check out their original glory. Anyone manage to find them?
- Secret
- Trionian
- Posts: 162
- Joined: Tue Jul 06, 2010 12:03 pm
Re: Particle Spin in 4d
Secret, check this one out:
http://winter.group.shef.ac.uk/orbitron/AOs/3d/equations.html
It seems to have many of the maths for orbital wave functions. It's also extremely cool.
http://winter.group.shef.ac.uk/orbitron/AOs/3d/equations.html
It seems to have many of the maths for orbital wave functions. It's also extremely cool.
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: Particle Spin in 4d
quickfur wrote:Rotations in 4D have some unusual characteristics not present in 3D.
The most prominent is the Clifford isoclinic rotation, in which the two orthogonal rotations proceed at an equal rate. When the two rotation rates are not equal, some points in the object will trace out spirals whereas those that lie on one of the stationary planes of the other rotation will trace out circles. So there are two distinguished stationary planes, orthogonal to each other, where points on the object will trace out circles. Outside of these two planes, points on the object will follow a non-circular spiralling path. However, in the isoclinic rotation, all points of the object trace out circles, and each of these circles lie in a stationary plane! So then there is an infinite number of stationary planes, and the original two orthogonal planes of rotation become indistinguishible from all the other stationary planes. The rotation therefore loses its distinctness in orientation: you could have started out with any orthogonal pair of rotations that lie in any corresponding pair of these infinite number of planes, and you'll get an identical rotation. So a whole bunch of rotations that would have been distinct, if the two rotation rates were different, have collapsed into a single isoclinic rotation.
However, this doesn't mean the rotation is completely independent of orientation! In fact, there are still an infinite number of distinct isoclinic rotations. They are produced if you rotate the planes of rotation along a direction that doesn't lie in any of its stationary planes. Furthermore, the isoclinic rotation is chiral -- there are two distinct "senses" of rotation given the same (infinite) set of stationary planes, and they cannot be reoriented into each other using only rigid motion. They are mirror images of each other.
Now, Wendy has mentioned before that any object that begins with two unequal rates of rotation will eventually settle into an isoclinic rotation via energy transfer -- because there is a gradient of different momentums in different parts of the object, that will prefer to equalize over time in order to reduce the total potential energy. So given any object in its natural state, it will basically always be found in an isoclinic rotation, rather than having two unequal rates of rotation. This suggests that 4D particles would be found with isoclinic spin in their ground state.
The interesting thing about this, is that the chirality of isoclinic rotations means that there are two possible such ground states, corresponding with the two possible chiralities of the isoclinic spin! So this seems to suggest an inherent two-charge or two-spin system, that arises purely from geometry alone!
so angular momentum is not conserved in four dimensions?
- granpa
- Dionian
- Posts: 20
- Joined: Sat Nov 10, 2012 12:21 am
Re: Particle Spin in 4d
Angular momentum is conserved in 4d although in 4d there is an extra degree of freedom so it is possible for something to spin in two independent directions.
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
- anderscolingustafson
- Tetronian
- Posts: 316
- Joined: Mon Mar 22, 2010 6:39 pm
Re: Particle Spin in 4d
anderscolingustafson wrote:In our Universe one of the fundamental properties of particles is their spin. In 3d it's only possible for a spinning object to have one independent direction of spin but in 4d it's possible for a spinning object to have two independent directions of spin. I was wondering would the fact that things can have a double rotation in 4d effect the fundamental spin of the fundamental particles?
The first thing to know is that quantum spin is NOT spin. It has only a superficial similarity to spin as we know it. An electron is a point particle with zero radius, nevertheless it has quantum spin.
Quantum spin has some quite weird properties. See the Stern-Gerlach experiment, which is simple but inexplicable in Newtonian terms.
Unlike spin, quantum spin is orientable. That is, quantum spin has the same sense no matter how the observer is oriented. Ordinary 3D spin does not have this property.
It is entirely possible that higher dimensional spaces are involved.
- PatrickPowers
- Tetronian
- Posts: 449
- Joined: Wed Dec 02, 2015 1:36 am
Re: Particle Spin in 4d
PatrickPowers wrote:
An electron is a point particle with zero radius, nevertheless it has quantum spin.
It's definitely not. The point paricle is only a mathematical approximation for practical purposes. In this sense even stars are point particles considering certain problems.
quickfur wrote:That diagram is certainly more accurate than tear-drop shaped orbital depictions (often employed in VSEPR theory).Nevertheless, the p orbitals are not ellipsoidal, as depicted here. They are more like dumbbell shapes. So this diagram probably still represents an artist's vision of the orbitals, rather than a mathematically accurate depiction.
Yes, here is a cut through the wave functions of the simplest orbitals. I think it's easier to get their shapes in 2D.

What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 136
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Particle Spin in 4d
For all intents and purposes, we can assume that the electron is a point particle. Experiments with single electrons in Penning traps have put an upper limit of 10−22 meters on the radius of the electron. That is 1/500000000000 of the Bohr radius of the hydrogen atom - it's very small. Being an upper limit, the electron could in fact be smaller than that, or it may actually be a point particle. Of course, a charged particle of vanishing radius is hard to describe theoretically, but nature is not bound by our theories.
https://www.quora.com/Is-electron-a-point-particle-as-assumed-in-Quantum-Mechanics
Be that as it may, an electron is too small for quantum spin to be explained as ordinary spin in 3+1D.
- PatrickPowers
- Tetronian
- Posts: 449
- Joined: Wed Dec 02, 2015 1:36 am
Re: Particle Spin in 4d
For all intents and purposes, we can assume that the electron is a point particle.
Not even that. Diffraction and interference is not explained by point-like particles. Matter is made up of standing waves with energy and momentum determined by the shape of those waves. A mere point-like particle wouldn't exhibit neither uncertainity principle nor Pauli principle and it wouldn't be stable orbiting an atom.
Experiments with single electrons in Penning traps have put an upper limit of 10−22 meters on the radius of the electron. That is 1/500000000000 of the Bohr radius of the hydrogen atom - it's very small.
The electron radius is a really misleading term and it's worthless without a definition. Which radius is the guy talking about? What's the experimental setup and the theory used? There are many ways to assign a radius to an electron. Most of them have a practical meaning, but the picture of the radius of a solid particle should not be taken too seriously and might be more deceptive than it helpful.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 136
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Particle Spin in 4d
Teragon wrote:For all intents and purposes, we can assume that the electron is a point particle.
Not even that. Diffraction and interference is not explained by point-like particles. Matter is made up of standing waves with energy and momentum determined by the shape of those waves. A mere point-like particle wouldn't exhibit neither uncertainity principle nor Pauli principle and it wouldn't be stable orbiting an atom.Experiments with single electrons in Penning traps have put an upper limit of 10−22 meters on the radius of the electron. That is 1/500000000000 of the Bohr radius of the hydrogen atom - it's very small.
The electron radius is a really misleading term and it's worthless without a definition. Which radius is the guy talking about? What's the experimental setup and the theory used? There are many ways to assign a radius to an electron. Most of them have a practical meaning, but the picture of the radius of a solid particle should not be taken too seriously and might be more deceptive than it helpful.
If these questions are of interest one might search for "experiments with single electrons in Penning traps." My intended point was that quantum spin is not the spinning of an object with a radius, as some might or might not mistakenly believe. It was not intended to imply or suggest that reader is or is not to be included in such company, nor was it intended to imply that the radius of an electron is a clearly defined concept.
One may further note that in the quantum world the word "particle" really means a "localized excitation of a field."
- PatrickPowers
- Tetronian
- Posts: 449
- Joined: Wed Dec 02, 2015 1:36 am
Re: Particle Spin in 4d
Be that as it may, an electron is too small for quantum spin to be explained as ordinary spin in 3+1D.
Although quantum spin is different from classical spin it is still effected by the number of dimensions which is why in 2+1 dimensions there are particles that have spin states that is neither integer nor none integer known as anyons but in any number of dimensions greater than 2 anyons cannot exist.
Unlike spin, quantum spin is orientable. That is, quantum spin has the same sense no matter how the observer is oriented. Ordinary 3D spin does not have this property.
The reason ordinary spin cannot be orientated in 3+1 dimensions is because ordinary objects don't move at the speed of light so that their direction of motion depends is not the same for all reference frames meaning that its helicity is depends on the reference frame. For an object that is moving at the speed of light in 3+1 dimensions its direction of motion is the same in all reference frames and so its helicity is also the same in all reference frames and so the spin has a chirality to it. A massless particle can never move slower than the speed of light but it can interact with other particles and that interaction can change its direction and if it changes direction then it will take longer to get from place to place than if it moves in a straight line and so it will appear to move at less than the speed of light which is how the Higgs Field works. Particles with mass are interacting with the Higgs Field all the time and so even though without the Higgs Boson it would move at the speed of light and so have a helicity the interaction with the Higgs Field causes it to appear to move slower than light but the spin remains chiral in spite of the particle having mass from the Higgs Field. So spin that has chirality that is the same in all reference frames is different from ordinary spin it actually can be explained by there being 3+1 dimensions for something moving at the speed of light, which is what massive particles would do if there was no Higgs Field.
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
- anderscolingustafson
- Tetronian
- Posts: 316
- Joined: Mon Mar 22, 2010 6:39 pm
Re: Particle Spin in 4d
quickfur wrote: Now, Wendy has mentioned before that any object that begins with two unequal rates of rotation will eventually settle into an isoclinic rotation via energy transfer -- because there is a gradient of different momentums in different parts of the object, that will prefer to equalize over time in order to reduce the total potential energy. So given any object in its natural state, it will basically always be found in an isoclinic rotation, rather than having two unequal rates of rotation. This suggests that 4D particles would be found with isoclinic spin in their ground state.
wendy wrote: A free particle in 4D would, by transfer of energy between modes, tend to assume a clifford-rotation.
granpa wrote: so angular momentum is not conserved in four dimensions?
Because of conservation of angular momentum, and a glome's symmetry (making the inertia tensor a scalar), an isolated glome spinning would maintain its angular velocity. It would not decay toward an isoclinic rotation. This has nothing to do with energy.
Do you mean that a non-isolated glome would interact with other objects in a way that favours isoclinic rotation?
ΓΔΘΛΞΠΣΦΨΩ αβγδεζηθϑικλμνξοπρϱσςτυϕφχψωϖ °±∓½⅓⅔¼¾×÷†‡• ⁰¹²³⁴⁵⁶⁷⁸⁹⁺⁻⁼⁽⁾₀₁₂₃₄₅₆₇₈₉₊₋₌₍₎
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
- mr_e_man
- Tetronian
- Posts: 489
- Joined: Tue Sep 18, 2018 4:10 am
Re: Particle Spin in 4d
mr_e_man wrote:quickfur wrote: Now, Wendy has mentioned before that any object that begins with two unequal rates of rotation will eventually settle into an isoclinic rotation via energy transfer -- because there is a gradient of different momentums in different parts of the object, that will prefer to equalize over time in order to reduce the total potential energy. So given any object in its natural state, it will basically always be found in an isoclinic rotation, rather than having two unequal rates of rotation. This suggests that 4D particles would be found with isoclinic spin in their ground state.wendy wrote: A free particle in 4D would, by transfer of energy between modes, tend to assume a clifford-rotation.granpa wrote: so angular momentum is not conserved in four dimensions?
Because of conservation of angular momentum, and a glome's symmetry (making the inertia tensor a scalar), an isolated glome spinning would maintain its angular velocity. It would not decay toward an isoclinic rotation. This has nothing to do with energy.
Do you mean that a non-isolated glome would interact with other objects in a way that favours isoclinic rotation?
This topic looks to be exactly related to my thread about the stability of orbits in spaces of dimension other than 3.
I believe that the confusion stems from the idea that angular momentum does not actually behave the same way in higher dimensions. The reason that angular momentum is a conserved quantity is because of rotational symmetry, as per Noether's theorem, but the way that rotation works gets upgraded every even dimension, meaning that the way angular momentum works should also be upgraded accordingly.
This should mean that an object in 4D or higher actually could have a transfer of rotation between/among its various orthogonal planes of rotation without violating the upgraded conservation of angular momentum of its dimension. In other words, higher dimensional angular momenta are increasingly "looser" because they expand into more and more orthogonal planes of rotation.
To be more specific about why such a transfer would occur, when there are multiple planes of rotation, different rates of rotation cause different points throughout the rotating object to have acceleration vectors pointing toward different central points, and it is only during an isoclinic rotation that all of the acceleration vectors agree on the center of rotation; although, in the odd dimensions, the leftover axis stretches the center of rotation into a line, meaning that an isoclinic rotation will still induce a squishing effect on the rotating object (like how, in 3D, rotating spheres want to squish down into disks). It is only in 2D where the acceleration vector of every point in a rotating object will always point toward the same central point.
With regard to the how, it is simply the binding forces of the object material that are actually responsible for these transfers. Different internal portions of the rotating object will pull on each other until isoclinic rotation is achieved, or at least as close as is possible according to the exact nature of the binding forces. For example, the internal stress created by the different rates of simultaneous rotation might not actually be great enough to overcome the rigidity of the object created by the binding forces. However, even this should still heat the object, which would slowly radiate the heat, which would carry away tiny amounts of angular momentum until the object really did settle into true isoclinism. However, in odd dimensions, if the rotating object has different cross-sections along the leftover axis (e.g. a sphere but not a cylinder), then this angular momentum leakage by way of heating from internal stress created by the rotation could continue asymptotically toward fully halting the rotation because of that squishing effect.
-

d023n - Dionian
- Posts: 35
- Joined: Sun Oct 01, 2017 10:16 pm
Re: Particle Spin in 4d
anderscolingustafson wrote:Be that as it may, an electron is too small for quantum spin to be explained as ordinary spin in 3+1D.
Although quantum spin is different from classical spin it is still effected by the number of dimensions which is why in 2+1 dimensions there are particles that have spin states that is neither integer nor none integer known as anyons but in any number of dimensions greater than 2 anyons cannot exist.
Truly a little-known fact.
The reason ordinary spin cannot be orientated in 3+1 dimensions is because ordinary objects don't move at the speed of light so that their direction of motion depends is not the same for all reference frames meaning that its helicity is depends on the reference frame. For an object that is moving at the speed of light in 3+1 dimensions its direction of motion is the same in all reference frames and so its helicity is also the same in all reference frames and so the spin has a chirality to it. A massless particle can never move slower than the speed of light but it can interact with other particles and that interaction can change its direction and if it changes direction then it will take longer to get from place to place than if it moves in a straight line and so it will appear to move at less than the speed of light which is how the Higgs Field works. Particles with mass are interacting with the Higgs Field all the time and so even though without the Higgs Boson it would move at the speed of light and so have a helicity the interaction with the Higgs Field causes it to appear to move slower than light but the spin remains chiral in spite of the particle having mass from the Higgs Field. So spin that has chirality that is the same in all reference frames is different from ordinary spin it actually can be explained by there being 3+1 dimensions for something moving at the speed of light, which is what massive particles would do if there was no Higgs Field.
I'm no expert but I believe that ALL quantum objects have orientable spin. Neutrinos, electrons, protons, even atoms. They don't have to be traveling at the speed of light.
The fact that quantum spin is orientable shows that it is an even-dimensional phenomenon. I think that it is not reasonable for time to be one of those dimensions. It seems to me that it isn't possible to make a complete, cyclic rotation with time one of the dimensions.
Last edited by PatrickPowers on Fri Jan 04, 2019 1:20 pm, edited 1 time in total.
- PatrickPowers
- Tetronian
- Posts: 449
- Joined: Wed Dec 02, 2015 1:36 am
Re: Particle Spin in 4d
viewtopic.php?f=27&t=1695#p26195
Angular momentum does not have the same units as energy. Energy is K = (1/2)m(v.v) (using the vector dot product), and angular momentum is L = mx^v (using the wedge product, and position vector x). There's a missing factor of time; v = dx/dt. Maybe you were thinking of torque, which does have the same units as energy, being dL/dt.
And they're different in other ways. Energy is a scalar; it has no orientation. Angular momentum is a bivector, having the orientation of a plane (or several planes in higher than 3D). An object in 4D does indeed have 2 orthogonal components of angular momentum, each of which is a simple bivector (representing one plane): L = L12e1e2+L34e3e4. (In general, there would be more terms, but we can simplify it to this by aligning our coordinate basis vectors ek with the rotation planes.)
A single classical point particle (no intrinsic spin) has only one plane of rotation (L34 = 0). A collection of particles has angular momentum equal to the sum of the individual particles' angular momenta: L = sum mx^v.
Angular momentum is conserved by any radial force (and Newton's laws): if two particles interact by a force F parallel to the displacement (x - x'), then dL/dt = d/dt(mx^v + m'x'^v') = md/dt(x^v) + m'd/dt(x'^v') = m(v^v + x^a) + m'(v'^v' + x'^a') = 0 + x^(ma) + 0 + x'^(m'a') = x^F + x'^(-F) = (x - x')^F = 0, thus L is constant.
An extended object's angular momentum is calculated by an integral over its mass (or volume, using density as conversion factor): L = int x^v dm.
The angular velocity bivector w of an object can be described with Geometric Algebra. Each point x in the object satisfies the differential equation dx/dt = x.w, which we can solve (assuming w is constant) using the exponential function: x = exp(-wt/2)x0exp(wt/2). Or we can plug it into the angular momentum integral, to get L = int x^(x.w) dm. Calculating this for a (solid) glome with radius r and mass m, we get L = (1/3)mr2w. This equation shows that if L is constant, then w is also constant. (Objects with less symmetry could have w precessing around the fixed L.)
With constant w = w12e1e2+w34e3e4, we can differentiate the differential equation to get a point's acceleration: a = d2x/dt2 = (dx/dt).w = (x.w).w, which expands to a = -(w12)2(x1e1+x2e2) -(w34)2(x3e3+x4e4). So you're correct about the acceleration pointing in different directions except for isoclinic rotations (w12)2 = (w34)2.
This reminds me of the https://en.wikipedia.org/wiki/Yarkovsky_effect
d023n wrote: Anyways, I was also considering that thinking in terms of angular momentum may be more helpful. It has the same units as energy after all, and I interpret it representing the amount of energy stored in the orbit. And then I remembered that in 4D there are 2 ways to simultaneously rotate, which made me think about orbitting 2 ways simultaneously. If an object is going around something using the XY plane, it still has the option to go around it using the ZW plane. Then it hit me.
It should have 2 orthogonal angular momenta! In fact, it makes sense to describe it as having 1 "double-angular" momentum that scales with the 4th power of the velocity, given that "single-angular" momentum scales with square of the velocity. This means that 4D still is not sufficient to achieve a stable orbit because gravity still scales with the inverse 3rd power of the distance, but 5D works!
Angular momentum does not have the same units as energy. Energy is K = (1/2)m(v.v) (using the vector dot product), and angular momentum is L = mx^v (using the wedge product, and position vector x). There's a missing factor of time; v = dx/dt. Maybe you were thinking of torque, which does have the same units as energy, being dL/dt.
And they're different in other ways. Energy is a scalar; it has no orientation. Angular momentum is a bivector, having the orientation of a plane (or several planes in higher than 3D). An object in 4D does indeed have 2 orthogonal components of angular momentum, each of which is a simple bivector (representing one plane): L = L12e1e2+L34e3e4. (In general, there would be more terms, but we can simplify it to this by aligning our coordinate basis vectors ek with the rotation planes.)
A single classical point particle (no intrinsic spin) has only one plane of rotation (L34 = 0). A collection of particles has angular momentum equal to the sum of the individual particles' angular momenta: L = sum mx^v.
Angular momentum is conserved by any radial force (and Newton's laws): if two particles interact by a force F parallel to the displacement (x - x'), then dL/dt = d/dt(mx^v + m'x'^v') = md/dt(x^v) + m'd/dt(x'^v') = m(v^v + x^a) + m'(v'^v' + x'^a') = 0 + x^(ma) + 0 + x'^(m'a') = x^F + x'^(-F) = (x - x')^F = 0, thus L is constant.
An extended object's angular momentum is calculated by an integral over its mass (or volume, using density as conversion factor): L = int x^v dm.
The angular velocity bivector w of an object can be described with Geometric Algebra. Each point x in the object satisfies the differential equation dx/dt = x.w, which we can solve (assuming w is constant) using the exponential function: x = exp(-wt/2)x0exp(wt/2). Or we can plug it into the angular momentum integral, to get L = int x^(x.w) dm. Calculating this for a (solid) glome with radius r and mass m, we get L = (1/3)mr2w. This equation shows that if L is constant, then w is also constant. (Objects with less symmetry could have w precessing around the fixed L.)
With constant w = w12e1e2+w34e3e4, we can differentiate the differential equation to get a point's acceleration: a = d2x/dt2 = (dx/dt).w = (x.w).w, which expands to a = -(w12)2(x1e1+x2e2) -(w34)2(x3e3+x4e4). So you're correct about the acceleration pointing in different directions except for isoclinic rotations (w12)2 = (w34)2.
However, even this should still heat the object, which would slowly radiate the heat, which would carry away tiny amounts of angular momentum until the object really did settle into true isoclinism. However, in odd dimensions, if the rotating object has different cross-sections along the leftover axis (e.g. a sphere but not a cylinder), then this angular momentum leakage by way of heating from internal stress created by the rotation could continue asymptotically toward fully halting the rotation because of that squishing effect.
This reminds me of the https://en.wikipedia.org/wiki/Yarkovsky_effect
ΓΔΘΛΞΠΣΦΨΩ αβγδεζηθϑικλμνξοπρϱσςτυϕφχψωϖ °±∓½⅓⅔¼¾×÷†‡• ⁰¹²³⁴⁵⁶⁷⁸⁹⁺⁻⁼⁽⁾₀₁₂₃₄₅₆₇₈₉₊₋₌₍₎
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
- mr_e_man
- Tetronian
- Posts: 489
- Joined: Tue Sep 18, 2018 4:10 am
Re: Particle Spin in 4d
mr_e_man wrote:Angular momentum does not have the same units as energy. Energy is K = (1/2)m(v.v) (using the vector dot product), and angular momentum is L = mx^v (using the wedge product, and position vector x). There's a missing factor of time; v = dx/dt. Maybe you were thinking of torque, which does have the same units as energy, being dL/dt.
Wow, you are exactly right. I make dumb mistakes like that more often than I would like, so I greatly appreciate your pointing that out to me. ^_^
Linear momentum has units of mass * distance / time, or mass * velocity.
Action and angular momentum have units of mass * distance2 / time, or
Force has units of mass * distance / time2, or mass * acceleration.
Energy and torque have units of mass * distance2 / time2, or
mr_e_man wrote:This reminds me of the https://en.wikipedia.org/wiki/Yarkovsky_effect
The Yarkovsky effect is a consequence of the fact that change in the temperature of an object warmed by radiation (and therefore the intensity of thermal radiation from the object) lags behind changes in the incoming radiation. That is, the surface of the object takes time to become warm when first illuminated; and takes time to cool down when illumination stops.
And then there's the https://en.wikipedia.org/wiki/Poynting-Robertson_effect
Last edited by d023n on Mon Oct 01, 2018 10:48 pm, edited 1 time in total.
-

d023n - Dionian
- Posts: 35
- Joined: Sun Oct 01, 2017 10:16 pm
Re: Particle Spin in 4d
Centre of mass has units of distance. Moment of mass has units of mass*distance.
ΓΔΘΛΞΠΣΦΨΩ αβγδεζηθϑικλμνξοπρϱσςτυϕφχψωϖ °±∓½⅓⅔¼¾×÷†‡• ⁰¹²³⁴⁵⁶⁷⁸⁹⁺⁻⁼⁽⁾₀₁₂₃₄₅₆₇₈₉₊₋₌₍₎
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
ℕℤℚℝℂ∂¬∀∃∅∆∇∈∉∋∌∏∑ ∗∘∙√∛∜∝∞∧∨∩∪∫≅≈≟≠≡≤≥⊂⊃⊆⊇ ⊕⊖⊗⊘⊙⌈⌉⌊⌋⌜⌝⌞⌟〈〉⟨⟩
- mr_e_man
- Tetronian
- Posts: 489
- Joined: Tue Sep 18, 2018 4:10 am
Re: Particle Spin in 4d
mr_e_man wrote:Centre of mass has units of distance. Moment of mass has units of mass*distance.
Ah, duh. Thanks again, moment is what I meant.
PatrickPowers wrote:anderscolingustafson wrote:In our Universe one of the fundamental properties of particles is their spin. In 3d it's only possible for a spinning object to have one independent direction of spin but in 4d it's possible for a spinning object to have two independent directions of spin. I was wondering would the fact that things can have a double rotation in 4d effect the fundamental spin of the fundamental particles?
The first thing to know is that quantum spin is NOT spin. It has only a superficial similarity to spin as we know it. An electron is a point particle with zero radius, nevertheless it has quantum spin.
Quantum spin has some quite weird properties. See the Stern-Gerlach experiment, which is simple but inexplicable in Newtonian terms.
Unlike spin, quantum spin is orientable. That is, quantum spin has the same sense no matter how the observer is oriented. Ordinary 3D spin does not have this property.
It is entirely possible that higher dimensional spaces are involved.
I was thinking recently that our universe might be an expanding 3-torus in a space of dimension 6 or higher. This would leave our universe spatially flat (as it appears to be) and might be an interesting direction for explaining things like dark matter and dark energy. Also, if the particles in our universe are actually higher dimensional objects whose locations and affects are just restricted to our 3-torus subspace (although dark matter might be affects from outside of the 3-torus, and dark energy would be expansion of the 3-torus), then quantum spin might really be genuine rotation but using the space outside of our 3-torus subspace. For example, in 3D, if the axis of rotation of a disc were to be treated as a 1D universe, the "1D particle" that is the disc's center might be thought of as having a sort of quantum spin that could have 2 different directions in the 1D universe depending on which way the disc is rotating in the full 3D universe. Also, this could explain why, as Patrick said, our own quantum spin is the same regardless of who is observing or from where.
-

d023n - Dionian
- Posts: 35
- Joined: Sun Oct 01, 2017 10:16 pm
Re: Particle Spin in 4d
Hi -- I am new here. There seem to be some insightful comments here and so I am enticed to post.
I am mostly just speaking out loud as that helps me organize my thoughts -- and I look forward to other comments this may inspire.
I have been studying, animating and experimenting with spin waves for over a decade now. For preference I call these waves spin solitons as they are quite capable of sustained solitary existence.
You can find some introductory material I wrote here https://www.chavascience.com/en/spin-lab/s-spinors -- this touches on a new method and syntax I have developed for describing spin solitons. *note: I have yet to publicly document another new formulation that has greater physical reality -- all spin soiltons can also be described with a set of nested librations. (a libration is an oscillatory rotation)
There appear to be an infinitely countable set of unique spin solitons in 3 dimensions... as there will be in any 3+ dimensions.
Experimental results confirm the mathematics of a 3D spin soliton as being the basis for electrons and protons -- they are the only stable spin solitons in our universe (neutrons are not stable -- they only have a 15min half life outside an atom).
As it can be seen - the 1/2 spin nature of the spin soliton arises from the folding of the kernel function which adds the counter rotations... and so we have a set of possible spins of 1/2n.
It is intuitively trivial to see where the spin 1/2n solitons arise from in 3D -- in this case spin arises from a folding of the kernel function -- effectively flipping the central rotation over. In 3D we have a single rotation plane plus one extra dimension to effect the folding over of the rotation...
So what happens in 4D where the dimensions are fully populated by 2 fully orthogonal 2D rotation planes -- leaving no odd dimensions to effect a fold in? ... clearly there can be two fully orthogonal spin functions that share a single fold dimension. Now as each fully orthogonal rotation plane serves as a oriented reference for the other we see that we can get 2 x 2 view independent spin combinations...
Explaining this another way -- with 4D dimensions x,y,z,w we can place the first spin soliton on x,y with fold in x,z -- in the syntax I have developed that's <s> with spin axis z. Now we can have a second spinor in 4D on z,w with fold in z,x say. ... this may not be obvious to anyone I realize -- but the result is that each of the spinors on two fully orthogonal rotation planes induce a radial phase advance or retardation in the center of the other fully orthogonal spinor. So again we see that here are 4 possible outcomes with each spinor being phase advanced or retarded.
So it appears that in 3D spin will still exhibit a 1/2 characteristic but will generate 4 distinct flavors. -- I didn't explain earlier but 3D spin falls into just two, positive and negative, classes as the inside phase may be advanced or retarded with respect to the outside.
Now what I find really interesting are the 4D spin solutions where the frequency of the two component rotations are in a PV ratio (PV - Pisot number - a subset of irrational numbers that includes the golden mean). PV ratios here lead to a number of interesting outcomes:
1. overall period is undefined while being composed of two pure harmonic components.
2. PV ratios lead to maximal energy loading in resonant systems, and minimum energy radiation.
3. 1,2 lead to an interesting outcome where from a 3D subset point of view a 4D spinor will appear to have a radially decaying pure broadband noise added to the spin axis... and the combination of harmonic (minimum total energy but maximal energy localization and radiation) and chaotic components will imply a net energy flow -- with 3D spin driven by noise.
So we are left with an intriguing possibility that some of the "quantum background noise" we see in spin solitons could be revealing a PV ratio frequency in a 4D spin soliton.
This is barely the beginning of my exploration of 4D spin. I believe it is much richer that I have alluded to here. The fundamental spin 1/2 3D spin soliton has a fold of the 2D rotation in a third dimension -- but in 4D the fold can occur in one of two orthogonal axis <s>,z <s>,w Theses, of course, can be superimposed. Given that we have a total of 6 combinations of axis to form rotation planes in 4D, and that each of these could have a kernel fold function in one of two orthogonal axis we end up with the possibility 12 fundamental spin orientations -- of which we can have combinations of any 1 - 4 at once. Clearly the combinations multiply quickly -- but what ones are likely? -- perhaps ring systems?
anyway -- more then enough for a first post.
If you got this far then thankyou for you attention and I look forward to any thoughts I may have provoked.
Cheers
Mark.
I am mostly just speaking out loud as that helps me organize my thoughts -- and I look forward to other comments this may inspire.
I have been studying, animating and experimenting with spin waves for over a decade now. For preference I call these waves spin solitons as they are quite capable of sustained solitary existence.
You can find some introductory material I wrote here https://www.chavascience.com/en/spin-lab/s-spinors -- this touches on a new method and syntax I have developed for describing spin solitons. *note: I have yet to publicly document another new formulation that has greater physical reality -- all spin soiltons can also be described with a set of nested librations. (a libration is an oscillatory rotation)
There appear to be an infinitely countable set of unique spin solitons in 3 dimensions... as there will be in any 3+ dimensions.
Experimental results confirm the mathematics of a 3D spin soliton as being the basis for electrons and protons -- they are the only stable spin solitons in our universe (neutrons are not stable -- they only have a 15min half life outside an atom).
As it can be seen - the 1/2 spin nature of the spin soliton arises from the folding of the kernel function which adds the counter rotations... and so we have a set of possible spins of 1/2n.
It is intuitively trivial to see where the spin 1/2n solitons arise from in 3D -- in this case spin arises from a folding of the kernel function -- effectively flipping the central rotation over. In 3D we have a single rotation plane plus one extra dimension to effect the folding over of the rotation...
So what happens in 4D where the dimensions are fully populated by 2 fully orthogonal 2D rotation planes -- leaving no odd dimensions to effect a fold in? ... clearly there can be two fully orthogonal spin functions that share a single fold dimension. Now as each fully orthogonal rotation plane serves as a oriented reference for the other we see that we can get 2 x 2 view independent spin combinations...
Explaining this another way -- with 4D dimensions x,y,z,w we can place the first spin soliton on x,y with fold in x,z -- in the syntax I have developed that's <s> with spin axis z. Now we can have a second spinor in 4D on z,w with fold in z,x say. ... this may not be obvious to anyone I realize -- but the result is that each of the spinors on two fully orthogonal rotation planes induce a radial phase advance or retardation in the center of the other fully orthogonal spinor. So again we see that here are 4 possible outcomes with each spinor being phase advanced or retarded.
So it appears that in 3D spin will still exhibit a 1/2 characteristic but will generate 4 distinct flavors. -- I didn't explain earlier but 3D spin falls into just two, positive and negative, classes as the inside phase may be advanced or retarded with respect to the outside.
Now what I find really interesting are the 4D spin solutions where the frequency of the two component rotations are in a PV ratio (PV - Pisot number - a subset of irrational numbers that includes the golden mean). PV ratios here lead to a number of interesting outcomes:
1. overall period is undefined while being composed of two pure harmonic components.
2. PV ratios lead to maximal energy loading in resonant systems, and minimum energy radiation.
3. 1,2 lead to an interesting outcome where from a 3D subset point of view a 4D spinor will appear to have a radially decaying pure broadband noise added to the spin axis... and the combination of harmonic (minimum total energy but maximal energy localization and radiation) and chaotic components will imply a net energy flow -- with 3D spin driven by noise.
So we are left with an intriguing possibility that some of the "quantum background noise" we see in spin solitons could be revealing a PV ratio frequency in a 4D spin soliton.
This is barely the beginning of my exploration of 4D spin. I believe it is much richer that I have alluded to here. The fundamental spin 1/2 3D spin soliton has a fold of the 2D rotation in a third dimension -- but in 4D the fold can occur in one of two orthogonal axis <s>,z <s>,w Theses, of course, can be superimposed. Given that we have a total of 6 combinations of axis to form rotation planes in 4D, and that each of these could have a kernel fold function in one of two orthogonal axis we end up with the possibility 12 fundamental spin orientations -- of which we can have combinations of any 1 - 4 at once. Clearly the combinations multiply quickly -- but what ones are likely? -- perhaps ring systems?
anyway -- more then enough for a first post.
If you got this far then thankyou for you attention and I look forward to any thoughts I may have provoked.
Cheers
Mark.
- marksnoswell
- Nullonian
- Posts: 1
- Joined: Fri Jan 04, 2019 3:51 am
Re: Particle Spin in 4d
I decided to look as spin as a kind of circulation of out-vector. This is thinking aloud, not really settled.
A line segment, as part of a larger line, can be regarded as <-------> ie a portion of a line space, bounded by two points. At each of these points, there is an outward pointing vector surface S. The content of this line is then the moment of surface, ie +(>)end-(<)end. When two lines are joined, you get <----><---->, the surface vectors cancel out in the middle.
A polygon is a closed segment of lines, where all of the end-points cancel out. In other words, there is no surface or transverse tension. But the 'circulation' of a line is made present, if that if we assume one transverser a line right-to-left, there is a 'cisverse' vector pointing 'upwards', and the outvector of a polygon is then these cisverse lines pointing 'outwards' from the polygon. The nature of a d1 polygon is that its out-vector points outwards from the polygon, and the circulation can be thought of as a surface current going from right to left of a polygon.
Two polygons joined together, would then on the joining edge, the current flows in equal amounts in both directions, and cancels out. So the effect of two polygons joined like this, is a current traveling around the exposed perimeter. As several more polygons are joined to this, there is always a constant circulation around the perimeter. Eventually, the polygons close, and we have then a polyhedron, for which any circuit on the surface has a current in each direction, so that the two regions have a positive space, and that viewed from the interior of each polygon, the current goes in the same anticlockwise way.
The right-hand rule is that if one points the direction of the circulation of a face in the direction of the fingers, the thumb points to the normal outvector or the cis-verse vector.
A polychoron, viewed from within, is bounded by polyhedra, which where one crosses the surface at some point inside the polyhedron, the faces of the polyhedron are anticlockwise, and so we can attrit circulation to any dimensional space, such circulation has an in-out direction in terms of some space it is solid in, and a general co-circulation of the same parity to any larger space. This examples as a line in 3d, has an inwards circulation of some sort of direction, and an around-circulation that points circles anticlockwise as in the right-hand rule. Likewise this complements that a surface, supposing anticlockwise circulation on the surface, has a normal in that dorection.
In four dimensions, a circle of given circulation produces an orthogonal circle by clifford-parallels, and there is one for each parity of cliffords. Likewise, a sphere of positive circulation produces a vector in a specific direction.
Circulation derived in the previous section is a fait of all dimensions. That is there is a transfer of surface to content circulation. The surface, divided by a marginix cut into two parts, will produce two areas of outvector +S and -S. This is true for all surfaces, so if we were to replace +S with a second surface bounded by the same marginix, the vector sum of its surface-normals will also be +S. This means that something like the magnetic moment m=IA, is true in all dimensions, where m is the magnetic moment, I is a measure of marginix-circulation (in 3d, this is a loop carrying current), and A is the vector-area (ie the sum of vectors representing the normals to the surface bounded by the marginix), is meaningful in all dimensions.
Spin
If we suppose that an electron is a positive-spin, then a ray drawn out of an electron would lead to anti-clockwise cycles on the surface.
An electron is never supposed to be +½ or -½ spin in nature, but rather the generic ½ spin. It is when electrons form an orbital that the two electrons might join to form a + and - ½spins. This would put the transverse outvector of an orbital at ease, so that the orbital is a polycell with up- and down- faces, in the around-space. In 3d, this would translate to d1 and d-1 densities of the electron. But we only see the spin as account of the zeeman-effect.
It would be interesting to see other results here, but i suspect that we are looking at some sort of spacing by h, that normalises the cis-vector to 0.
As i said, i'm just playing around with ideas.
A line segment, as part of a larger line, can be regarded as <-------> ie a portion of a line space, bounded by two points. At each of these points, there is an outward pointing vector surface S. The content of this line is then the moment of surface, ie +(>)end-(<)end. When two lines are joined, you get <----><---->, the surface vectors cancel out in the middle.
A polygon is a closed segment of lines, where all of the end-points cancel out. In other words, there is no surface or transverse tension. But the 'circulation' of a line is made present, if that if we assume one transverser a line right-to-left, there is a 'cisverse' vector pointing 'upwards', and the outvector of a polygon is then these cisverse lines pointing 'outwards' from the polygon. The nature of a d1 polygon is that its out-vector points outwards from the polygon, and the circulation can be thought of as a surface current going from right to left of a polygon.
Two polygons joined together, would then on the joining edge, the current flows in equal amounts in both directions, and cancels out. So the effect of two polygons joined like this, is a current traveling around the exposed perimeter. As several more polygons are joined to this, there is always a constant circulation around the perimeter. Eventually, the polygons close, and we have then a polyhedron, for which any circuit on the surface has a current in each direction, so that the two regions have a positive space, and that viewed from the interior of each polygon, the current goes in the same anticlockwise way.
The right-hand rule is that if one points the direction of the circulation of a face in the direction of the fingers, the thumb points to the normal outvector or the cis-verse vector.
A polychoron, viewed from within, is bounded by polyhedra, which where one crosses the surface at some point inside the polyhedron, the faces of the polyhedron are anticlockwise, and so we can attrit circulation to any dimensional space, such circulation has an in-out direction in terms of some space it is solid in, and a general co-circulation of the same parity to any larger space. This examples as a line in 3d, has an inwards circulation of some sort of direction, and an around-circulation that points circles anticlockwise as in the right-hand rule. Likewise this complements that a surface, supposing anticlockwise circulation on the surface, has a normal in that dorection.
In four dimensions, a circle of given circulation produces an orthogonal circle by clifford-parallels, and there is one for each parity of cliffords. Likewise, a sphere of positive circulation produces a vector in a specific direction.
Circulation derived in the previous section is a fait of all dimensions. That is there is a transfer of surface to content circulation. The surface, divided by a marginix cut into two parts, will produce two areas of outvector +S and -S. This is true for all surfaces, so if we were to replace +S with a second surface bounded by the same marginix, the vector sum of its surface-normals will also be +S. This means that something like the magnetic moment m=IA, is true in all dimensions, where m is the magnetic moment, I is a measure of marginix-circulation (in 3d, this is a loop carrying current), and A is the vector-area (ie the sum of vectors representing the normals to the surface bounded by the marginix), is meaningful in all dimensions.
Spin
If we suppose that an electron is a positive-spin, then a ray drawn out of an electron would lead to anti-clockwise cycles on the surface.
An electron is never supposed to be +½ or -½ spin in nature, but rather the generic ½ spin. It is when electrons form an orbital that the two electrons might join to form a + and - ½spins. This would put the transverse outvector of an orbital at ease, so that the orbital is a polycell with up- and down- faces, in the around-space. In 3d, this would translate to d1 and d-1 densities of the electron. But we only see the spin as account of the zeeman-effect.
It would be interesting to see other results here, but i suspect that we are looking at some sort of spacing by h, that normalises the cis-vector to 0.
As i said, i'm just playing around with ideas.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2014
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
28 posts
• Page 1 of 1
Return to Higher Spatial Dimensions
Who is online
Users browsing this forum: No registered users and 3 guests
