Quickfur's renders
Re: Quickfur's renders
I've been writing in C++ / OpenGL for years. It's relatively quick, C++/C# are highly versatile, and even though the GL APIs are ancient it still makes more sense than DirectX, and it's easier than finding a rendering program that I can do what I want in. There's probably a way to get GL running in VB if C++ is too daunting, but I haven't tried it, and I love C++. Haven't gotten it working in C# either, but I haven't tried much or had the reason to.
- phoenix
- Mononian
- Posts: 5
- Joined: Fri Jan 13, 2012 3:10 am
Re: Quickfur's renders
Haven't been active on this forum for a while, but it is that time of the month again when I present a new Polytope of the Month. So this month, it's:

The rectified tesseract, a comparatively simple uniform polychoron, but nonetheless a mind-boggler when it comes to animations.

The rectified tesseract, a comparatively simple uniform polychoron, but nonetheless a mind-boggler when it comes to animations.

- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Quickfur's renders
May's polytope of the month is ...

The runcitruncated 24-cell! This cute little baby has 24 truncated octahedra (shown in red and yellow above) and 24 rhombicuboctahedra (shown in green above), with the gaps in between filled by 96 hexagonal prisms and 96 triangular prisms.
Interestingly enough, you can inscribe an omnitruncated tesseract in this polytope. If you squint at the above image, you can almost see the outline of an inscribed omnitruncated tesseract. It's essentially an omnitruncated tesseract whose octagonal prisms have been extended into rhombicuboctahedra, with the result that you build a cupola-like structure over the original great rhombicuboctahedra with more hexagonal prisms and triangular prisms, capped with truncated octahedra.
It's a pity there's no equivalent relationship between two uniform 3D polyhedra, otherwise I could show the analogous process in 3D; the process I described is very straightforward, but it's just hard to put into words.

The runcitruncated 24-cell! This cute little baby has 24 truncated octahedra (shown in red and yellow above) and 24 rhombicuboctahedra (shown in green above), with the gaps in between filled by 96 hexagonal prisms and 96 triangular prisms.
Interestingly enough, you can inscribe an omnitruncated tesseract in this polytope. If you squint at the above image, you can almost see the outline of an inscribed omnitruncated tesseract. It's essentially an omnitruncated tesseract whose octagonal prisms have been extended into rhombicuboctahedra, with the result that you build a cupola-like structure over the original great rhombicuboctahedra with more hexagonal prisms and triangular prisms, capped with truncated octahedra.
It's a pity there's no equivalent relationship between two uniform 3D polyhedra, otherwise I could show the analogous process in 3D; the process I described is very straightforward, but it's just hard to put into words.
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Quickfur's renders
quickfur wrote:Haven't been active on this forum for a while, but it is that time of the month again when I present a new Polytope of the Month. So this month, it's:
The rectified tesseract, a comparatively simple uniform polychoron, but nonetheless a mind-boggler when it comes to animations.
Ooh, that's a beauty

-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Quickfur's renders

 Keiji's alive!
Keiji's alive! 
Thanks for the compliment.
Unrelated note: I seem to have lost all email notifications from this forum (which is the reason for my recent untimely replies). Did some setting get mixed up in my profile, or is it another breakage caused by the move?
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Quickfur's renders
Check your PMs please.
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Quickfur's renders
Man, is it quiet in here. Well, let's remedy that with a 120-cell family polychoron:

This is the cantitruncated 600-cell, having 120 truncated icosahedra, 600 truncated octahedra (aka omnitruncated tetrahedron), and 720 pentagonal prisms.
Remember the bitruncated 120-cell? If you expand its truncated icosahedral cells outwards radially, you can fill in the gaps with truncated octahedra and pentagonal prisms to form the cantitruncated 600-cell.

This is the cantitruncated 600-cell, having 120 truncated icosahedra, 600 truncated octahedra (aka omnitruncated tetrahedron), and 720 pentagonal prisms.
Remember the bitruncated 120-cell? If you expand its truncated icosahedral cells outwards radially, you can fill in the gaps with truncated octahedra and pentagonal prisms to form the cantitruncated 600-cell.
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Quickfur's renders
It's that time of the month again, and here's my polytope of the month:

This month I decided to go against the tradition of posting a uniform polytope, and went for a CRF polychoron just for the heck of it. This one is the bi-tetraicosidiminished 600-cell, consisting of 48 tridiminished icosahedra. Before you dismiss this little pretty as non-symmetric and therefore boring, I'd like to state that it is both cell-transitive and vertex-transitive, so it's a lot more symmetrical than your typical CRF.
What's really cool, though --- and I discovered this while working on the structure renders --- is to discover just what sort of symmetry it has. You see, the tridiminished icosahedron is rather irregular; it only has a 3-fold symmetry around a single axis. And a cursory look at this polytope didn't boost my confidence either: the usual projection angles all turned up pretty irregular, and when I tried to graph the connectivities between the cells (vertex/edge/ridge connectivities, with the help of my program) I got various odd-looking graphs, sometimes with some hint of symmetry (mainly bilateral symmetry only, with irregular-looking halves -- not encouraging), but nowhere close to anything you can even call uniform or quasi-uniform.
But when I started doing the cell-by-cell renders, and arbitrarily decided to follow along chains of cells connected along the tridiminished icosahedron's sole axis of symmetry, a pattern began to emerge. First, there was a single line of 3 cells, joined end-to-end (if you imagine orienting the tridiminished icosahedron such that the triangular face surrounded by 3 pentagons is at the top, and its opposite triangular face, surrounded by 3 triangles, is at the bottom, then in the polytope there are chains of cells stacked top-to-bottom in this orientation). Which is nothing unusual -- I mean, this is after all the only axis of symmetry of the tridiminished icosahedron, so it's barely surprising that cells would line up accordingly.
When things started getting interesting, was when I then looked at cells attached to the side faces of this chain: they were oriented in a skew orientation, and at first my heart sank that it will just turn out to be a highly irregular arrangement, but as I started tracing the chains that these "side cells" were part of, I suddenly noticed that my first vertical line of 3 cells were being wrapped around by three other chains, in a corkscrew fashion. And these other chains were themselves wrapped by another three chains, also in a corkscrew fashion, except at a shallower angle. And eventually at the equator, was a 6-membered ring circling the original chain in a perpendicular plane.
And that was when it hit me: this is nothing less than the Hopf fibration of the 3-sphere!! Each chain is actually a ring of 6 cells each, and there are 8 rings in total. Every ring is "wrapped" by 3 other rings in a corkscrew fashion, which are in turn wrapped by another 3 rings at a shallower angle, which are in turn girded by the perpendicular ring. Together, these 8 rings completely cover up the surface of the polytope.
In other words, this polytope has swirlprism symmetry, and is directly related to Jonathan Bowers' polytwisters. The rings "swirl" around the surface of the polytope in a chiral way. Every ring is equivalent to every other ring, and every cell in each ring is also equivalent. So the rings are transitive, and so are the cells.
So, this irregular-looking CRF polychoron turns out to have quite an awesome symmetry after all!

This month I decided to go against the tradition of posting a uniform polytope, and went for a CRF polychoron just for the heck of it. This one is the bi-tetraicosidiminished 600-cell, consisting of 48 tridiminished icosahedra. Before you dismiss this little pretty as non-symmetric and therefore boring, I'd like to state that it is both cell-transitive and vertex-transitive, so it's a lot more symmetrical than your typical CRF.
What's really cool, though --- and I discovered this while working on the structure renders --- is to discover just what sort of symmetry it has. You see, the tridiminished icosahedron is rather irregular; it only has a 3-fold symmetry around a single axis. And a cursory look at this polytope didn't boost my confidence either: the usual projection angles all turned up pretty irregular, and when I tried to graph the connectivities between the cells (vertex/edge/ridge connectivities, with the help of my program) I got various odd-looking graphs, sometimes with some hint of symmetry (mainly bilateral symmetry only, with irregular-looking halves -- not encouraging), but nowhere close to anything you can even call uniform or quasi-uniform.
But when I started doing the cell-by-cell renders, and arbitrarily decided to follow along chains of cells connected along the tridiminished icosahedron's sole axis of symmetry, a pattern began to emerge. First, there was a single line of 3 cells, joined end-to-end (if you imagine orienting the tridiminished icosahedron such that the triangular face surrounded by 3 pentagons is at the top, and its opposite triangular face, surrounded by 3 triangles, is at the bottom, then in the polytope there are chains of cells stacked top-to-bottom in this orientation). Which is nothing unusual -- I mean, this is after all the only axis of symmetry of the tridiminished icosahedron, so it's barely surprising that cells would line up accordingly.
When things started getting interesting, was when I then looked at cells attached to the side faces of this chain: they were oriented in a skew orientation, and at first my heart sank that it will just turn out to be a highly irregular arrangement, but as I started tracing the chains that these "side cells" were part of, I suddenly noticed that my first vertical line of 3 cells were being wrapped around by three other chains, in a corkscrew fashion. And these other chains were themselves wrapped by another three chains, also in a corkscrew fashion, except at a shallower angle. And eventually at the equator, was a 6-membered ring circling the original chain in a perpendicular plane.
And that was when it hit me: this is nothing less than the Hopf fibration of the 3-sphere!! Each chain is actually a ring of 6 cells each, and there are 8 rings in total. Every ring is "wrapped" by 3 other rings in a corkscrew fashion, which are in turn wrapped by another 3 rings at a shallower angle, which are in turn girded by the perpendicular ring. Together, these 8 rings completely cover up the surface of the polytope.
In other words, this polytope has swirlprism symmetry, and is directly related to Jonathan Bowers' polytwisters. The rings "swirl" around the surface of the polytope in a chiral way. Every ring is equivalent to every other ring, and every cell in each ring is also equivalent. So the rings are transitive, and so are the cells.
So, this irregular-looking CRF polychoron turns out to have quite an awesome symmetry after all!
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Quickfur's renders
Hmm, apparently I forgot to post this month's polytope of the month here:

This is the runcitruncated 16-cell, a cute little thing with 8 rhombicuboctahedra, 16 truncated tetrahedra, 24 cubes, and 32 hexagonal prisms. Its Coxeter-Dynkin diagram is x4o3x3x (using Wendy's notation).

This is the runcitruncated 16-cell, a cute little thing with 8 rhombicuboctahedra, 16 truncated tetrahedra, 24 cubes, and 32 hexagonal prisms. Its Coxeter-Dynkin diagram is x4o3x3x (using Wendy's notation).
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Quickfur's renders
quickfur wrote:
...
In other words, this polytope has swirlprism symmetry, and is directly related to Jonathan Bowers' polytwisters. The rings "swirl" around the surface of the polytope in a chiral way. Every ring is equivalent to every other ring, and every cell in each ring is also equivalent. So the rings are transitive, and so are the cells.
So, this irregular-looking CRF polychoron turns out to have quite an awesome symmetry after all!
Can you do an animation of it rotating so that one ring becomes an equivalent ring and so on? With one ring highlighted.
Also can you do an animation looking down the original axis of symmetry you found, rotating through zw ("turning inside out")? With one group of three equivalent cells in the symmetry highlighted.
Not sure if that described it well enough, but they could help visualise

-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Quickfur's renders
Keiji wrote:[...]
Can you do an animation of it rotating so that one ring becomes an equivalent ring and so on? With one ring highlighted.
Hmm, this is a tough one; it requires a kind of skew rotation to transform one ring into another. I'll need a bit more time to figure out how to do it.
Also can you do an animation looking down the original axis of symmetry you found, rotating through zw ("turning inside out")? With one group of three equivalent cells in the symmetry highlighted.
Not sure if that described it well enough, but they could help visualise
OK, here's a first crack at it:
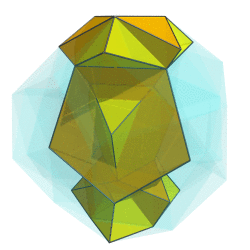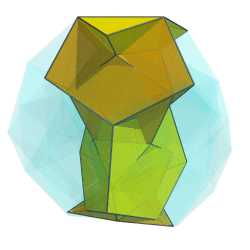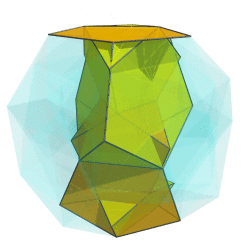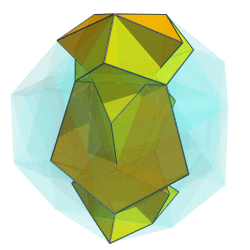
I can't say it looks very helpful, though. Any ideas on how to improve it?
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Quickfur's renders
quickfur wrote:I can't say it looks very helpful, though. Any ideas on how to improve it?
That's not exactly what I was looking for - if you take that orientation and rotate it 90 degrees around the y axis, then adjust the animation so it's "turning inside out" with the "middle" coming towards/away from the screen, that would be what I was imagining. Hopefully this is a better description

-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Quickfur's renders
Keiji wrote:quickfur wrote:I can't say it looks very helpful, though. Any ideas on how to improve it?
That's not exactly what I was looking for - if you take that orientation and rotate it 90 degrees around the y axis, then adjust the animation so it's "turning inside out" with the "middle" coming towards/away from the screen, that would be what I was imagining. Hopefully this is a better description
You mean like this?
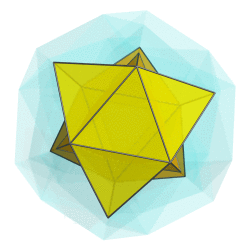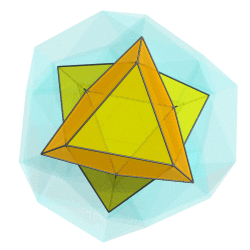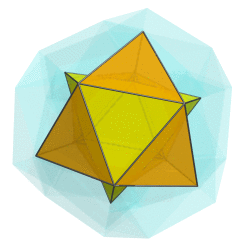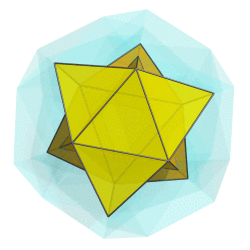
But somehow I don't think that's what you have in mind.
Or are you thinking of rotating along a different plane?
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Quickfur's renders
Okay, I give up - I have no idea what this polytope is supposed to be. 

-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Quickfur's renders
Keiji wrote:Okay, I give up - I have no idea what this polytope is supposed to be.
Hmm. Did you see the structure projections of it on my website? 'cos the image I posted above was from before I realized its symmetry, so it's not exactly the most helpful projection.
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Quickfur's renders
Okay, finally bothered to read the entire page... wish I'd done that sooner, it's a beautiful shape! 
I would call it the bixylodiminished hydrochoron, though
A little more concise than bi-icositetradiminished six-hundred-cell...
I wonder if I can get my head around it enough to figure out what its FLD should be... It should be a fairly compact one, given that it's cell transitive... hmm...

I would call it the bixylodiminished hydrochoron, though

A little more concise than bi-icositetradiminished six-hundred-cell...
I wonder if I can get my head around it enough to figure out what its FLD should be... It should be a fairly compact one, given that it's cell transitive... hmm...
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Quickfur's renders
Keiji wrote:Okay, finally bothered to read the entire page... wish I'd done that sooner, it's a beautiful shape!
I probably should redo that image so that it's more clear what the structure is. Maybe I can do two orthogonal rings, or the vertical ring plus one of the shallow rings. Putting everything in at once is kinda hard to see from our disadvantaged 3D viewpoint.

I would call it the bixylodiminished hydrochoron, though
A little more concise than bi-icositetradiminished six-hundred-cell...
Yeah, I'd adopt that too, except that then I'd lose search engine rank for not having the more common keywords. (Not that it matters in this case anyway -- I can't imagine a random web surfer typing in "biicositetradiminished" out of the blue -- but I'd like the names to be consistent with the more well-known objects, like "600-cell".)
Or maybe I should just come up with pet names for everything like Bowers does, and just reference the technical name somewhere on the page.
I wonder if I can get my head around it enough to figure out what its FLD should be... It should be a fairly compact one, given that it's cell transitive... hmm...
What's FLD?
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Quickfur's renders
quickfur wrote:Keiji wrote:Okay, finally bothered to read the entire page... wish I'd done that sooner, it's a beautiful shape!
I probably should redo that image so that it's more clear what the structure is. Maybe I can do two orthogonal rings, or the vertical ring plus one of the shallow rings. Putting everything in at once is kinda hard to see from our disadvantaged 3D viewpoint.
Actually, why not color the 8 rings accordingly: black/white, red/cyan, green/magenta, blue/yellow, where each ring is perpendicular to the ring of the inverse color. I'd like to see all cells highlighted in those colors. Maybe having this coloration do a Clifford rotation would be good? Can't know til you try.

I would call it the bixylodiminished hydrochoron, though
A little more concise than bi-icositetradiminished six-hundred-cell...
Yeah, I'd adopt that too, except that then I'd lose search engine rank for not having the more common keywords. (Not that it matters in this case anyway -- I can't imagine a random web surfer typing in "biicositetradiminished" out of the blue -- but I'd like the names to be consistent with the more well-known objects, like "600-cell".)
Or maybe I should just come up with pet names for everything like Bowers does, and just reference the technical name somewhere on the page.
Yes, I don't think Google rankings is the important thing here - just look how many of the top 10 slots we already have for crf polychora - the top two are here, and the next seven are your site (the last one is Wikipedia). Certainly for the topic of newly discovered polytopes, people will much more likely be searching for generic terms like that than names we've only just come up with.

What's FLD?
Facet Layout Diagram
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Quickfur's renders
I've just added the Bixylodiminished hydrochoron page, I'd appreciate if you checked it for accuracy, especially the element counts and how I arrive at them.
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Quickfur's renders
Keiji wrote:quickfur wrote:Keiji wrote:Okay, finally bothered to read the entire page... wish I'd done that sooner, it's a beautiful shape!
I probably should redo that image so that it's more clear what the structure is. Maybe I can do two orthogonal rings, or the vertical ring plus one of the shallow rings. Putting everything in at once is kinda hard to see from our disadvantaged 3D viewpoint.
Actually, why not color the 8 rings accordingly: black/white, red/cyan, green/magenta, blue/yellow, where each ring is perpendicular to the ring of the inverse color. I'd like to see all cells highlighted in those colors. Maybe having this coloration do a Clifford rotation would be good? Can't know til you try.
Ah, but the problem is that we aren't actually rendering cells per se, but ridges. Ridges have this inconvenient property of being shared by two cells
 so there is no easy way to show a distinct color for every cell.
so there is no easy way to show a distinct color for every cell.One thing that can be done, which is a bit hackish (but I use it all the time to tweak projection images), is to break up the ridges of the cells so that the innermost cells in the projection take priority over each subsequent layer, so a cell between the innermost and outermost will have half its ridges with the color of the previous layer's cell and the other half with the color logically assigned to it. But this approach doesn't work well for the equatorial ring, because in parallel projection you'll end up with coincident ridges that have different colors -- the perfect recipe for povray artifacts to show up loud and clear.

I would call it the bixylodiminished hydrochoron, though
A little more concise than bi-icositetradiminished six-hundred-cell...
Yeah, I'd adopt that too, except that then I'd lose search engine rank for not having the more common keywords. (Not that it matters in this case anyway -- I can't imagine a random web surfer typing in "biicositetradiminished" out of the blue -- but I'd like the names to be consistent with the more well-known objects, like "600-cell".)
Or maybe I should just come up with pet names for everything like Bowers does, and just reference the technical name somewhere on the page.
Yes, I don't think Google rankings is the important thing here - just look how many of the top 10 slots we already have for crf polychora - the top two are here, and the next seven are your site (the last one is Wikipedia). Certainly for the topic of newly discovered polytopes, people will much more likely be searching for generic terms like that than names we've only just come up with.
I'm kinda on the fence about the whole nomenclature issue.
On the one hand, my visitors aren't just people looking for CRFs,
 and I'd like to avoid inventing too many names for things which already have a name (even if I'm not particularly pleased with the existing name(s)). I don't mind using pet names and shorthands in discussion forums, because you can actively explain an odd name if a newbie is confused, but I find it a bit awkward to, for example, title my page on the truncated icosahedron as "Buckyball".
and I'd like to avoid inventing too many names for things which already have a name (even if I'm not particularly pleased with the existing name(s)). I don't mind using pet names and shorthands in discussion forums, because you can actively explain an odd name if a newbie is confused, but I find it a bit awkward to, for example, title my page on the truncated icosahedron as "Buckyball".But on the other hand, some of these names really are too long and too verbose. Like "hecatonicosichoron". Worse if you start prefixing adjectives like "cantiruncibouncytruncated". Not to mention that most of the conventional names are not fully consistent -- for example, terms like "bidiminished" and "tridiminished" count the number of cuttings made to the base polychoron, but what if there's more than one thing that can be cut off? The cantellated tesseract (x4o3x3o), for example, can be cut in thirds to form cuboctahedron||truncated_cube and truncated cube prism, but you can also cut off square magnabicupolic rings from it. There's no easy way to indicate this in the conventional naming scheme. Also, this is inconsistent from things like "bi-tetraicosidiminished", which refers not to the cutting off of any CRF pieces per se, but to the removal of a certain number of vertices.
And then things like Wendy's bistratic CRF with 4 tridiminished icosahedra, 5 tetrahedra, and 1 octahedron: I don't even know how to name such a thing except using Wendy's notation, but I find a bit hard to swallow that the title of the page would have to be "xfo3oox3ooo". There's no question her notation scheme is extremely powerful and expressive, but it doesn't give us pronunciable names.
So I can't decide one way or the other. :-(
Ah! I'll have to look at that a bit more closely later.
Keiji wrote:I've just added the Bixylodiminished hydrochoron page, I'd appreciate if you checked it for accuracy, especially the element counts and how I arrive at them.
I think your edge count is wrong: the polychoron only has 216 edges. But I don't have a quick way of finding out what the right numbers are, since my viewer doesn't really have a way of counting edge types at the moment.
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Quickfur's renders
Sometimes I talk too much. Let's remedy that with a two-ring animation of the bi-whatever-diminished 600-cell:
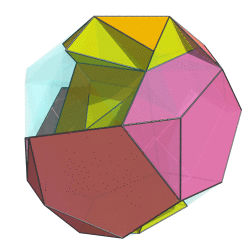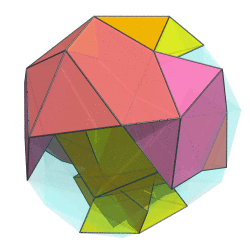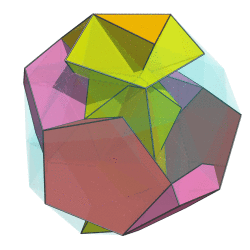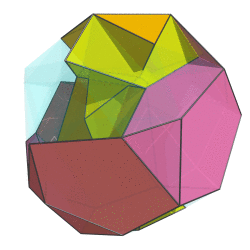
Not quite the full 6-ring animation, but this already looks cool beyond words. If I do say so myself. The way the red ring folds upon itself as it flips over in 4D is just tantalizing...
The way the red ring folds upon itself as it flips over in 4D is just tantalizing...

Not quite the full 6-ring animation, but this already looks cool beyond words. If I do say so myself.
 The way the red ring folds upon itself as it flips over in 4D is just tantalizing...
The way the red ring folds upon itself as it flips over in 4D is just tantalizing...- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Quickfur's renders
quickfur wrote:[...]And then things like Wendy's bistratic CRF with 4 tridiminished icosahedra, 5 tetrahedra, and 1 octahedron: I don't even know how to name such a thing except using Wendy's notation, but I find a bit hard to swallow that the title of the page would have to be "xfo3oox3ooo". There's no question her notation scheme is extremely powerful and expressive, but it doesn't give us pronunciable names.
[...]
Well, Wendy was just extrapolating into higher dimensions: xfo (or better xfo&#xt, to show what is meant really: a lace tower with unit edge (i.e. x) lacings (i.e. #)) is nothing but the regular pentagon. xfo3oox&#xt is nothing but the 3-diminished icosahedron. And then the next would be xfo3oox3ooo&#xt, which you have rendered, and now are asking for. So a pronouncable name could be "a 3-diminished icosahedron equivalent of 4D". Or you could get it even more funny, if you'd use Jonathans acronym instead: tridiminished icosahedron --> teddi: "Teddy in 4D"

- Klitzing
- Pentonian
- Posts: 1638
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Quickfur's renders
Klitzing wrote:quickfur wrote:[...]And then things like Wendy's bistratic CRF with 4 tridiminished icosahedra, 5 tetrahedra, and 1 octahedron: I don't even know how to name such a thing except using Wendy's notation, but I find a bit hard to swallow that the title of the page would have to be "xfo3oox3ooo". There's no question her notation scheme is extremely powerful and expressive, but it doesn't give us pronunciable names.
[...]
Well, Wendy was just extrapolating into higher dimensions: xfo (or better xfo&#xt, to show what is meant really: a lace tower with unit edge (i.e. x) lacings (i.e. #)) is nothing but the regular pentagon. xfo3oox&#xt is nothing but the 3-diminished icosahedron. And then the next would be xfo3oox3ooo&#xt, which you have rendered, and now are asking for. So a pronouncable name could be "a 3-diminished icosahedron equivalent of 4D". Or you could get it even more funny, if you'd use Jonathans acronym instead: tridiminished icosahedron --> teddi: "Teddy in 4D"
True, I could use a name like "4D tridiminished icosahedron", much like the 600-cell can be called "4D icosahedron", though that doesn't really do justice to the 600-cell's actual structure.

As for "teddi", I think I shall have to refer to xfo3oox3ooo&#xt as Teddy from now on.
 For the official name of the page ('cos I am planning to make a page for it on my website -- it's such an amazingly cool shape!), though, maybe I can abuse your vertical bar notation a bit, and call it something like tetrahedron||phi-tetrahedron||octahedron. It's still an overly-long name, though.
For the official name of the page ('cos I am planning to make a page for it on my website -- it's such an amazingly cool shape!), though, maybe I can abuse your vertical bar notation a bit, and call it something like tetrahedron||phi-tetrahedron||octahedron. It's still an overly-long name, though.  I can perhaps abbreviate the polyhedra names with my Coxeter-Dynkin-diagram-derived notation, A100||phi-A100||A101. A bit better, but still not good enough for my tastes.
I can perhaps abbreviate the polyhedra names with my Coxeter-Dynkin-diagram-derived notation, A100||phi-A100||A101. A bit better, but still not good enough for my tastes. 
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Quickfur's renders
I'll have a go at naming the shape... after you get the page up so that I can understand what it is. 
PS. Quickfur - any ideas what's wrong with my edge count calculations? I'm not sure how you got 216 edges, but it's also the first time I've calculate number of edges the way I did - though I can't see any reason why my method wouldn't work.

PS. Quickfur - any ideas what's wrong with my edge count calculations? I'm not sure how you got 216 edges, but it's also the first time I've calculate number of edges the way I did - though I can't see any reason why my method wouldn't work.
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Quickfur's renders
Keiji wrote:I'll have a go at naming the shape... after you get the page up so that I can understand what it is.
Well, this projection image that I posted in the other thread might help:
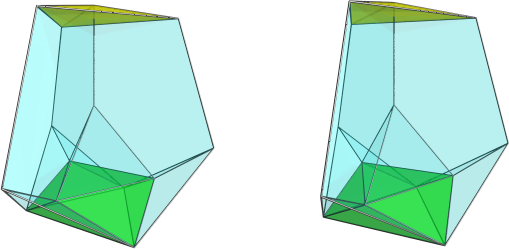
If you can do cross-eyed viewing, the 3D shape of the projection should be even more helpful.
It consists of 4 tridiminished icosahedra in tetrahedral formation, arranged around the top cell which is a tetrahedron, and at the bottom is an octahedron with 4 tetrahedra filling in the gaps between the bases of the tridiminished icosahedra. A really cute little shape. Teddy.

PS. Quickfur - any ideas what's wrong with my edge count calculations? I'm not sure how you got 216 edges, but it's also the first time I've calculate number of edges the way I did - though I can't see any reason why my method wouldn't work.
I didn't count the edges myself; I got 216 edges from the convex hull algorithm that I use to construct the model that my viewer uses to do the projection. I don't know what went wrong with your edge count calculations, it seems reasonable to me. But counting things in higher-dimensional polytopes has always been a tricky business. I mean, I have enough trouble with counting elements correctly in 3D polyhedra, let alone 4D.
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Quickfur's renders
quickfur wrote:[..] It consists of 4 tridiminished icosahedra in tetrahedral formation, arranged around the top cell which is a tetrahedron, and at the bottom is an octahedron with 4 tetrahedra filling in the gaps between the bases of the tridiminished icosahedra. A really cute little shape. Teddy.[...]
And I should add that the reason for calling it "4D tridiminished icosahedron" is because the top tetrahedron is analogous to the top face of the tridiminished icosahedron -- for reference, I'm using this orientation for the tridiminished icosahedron:

Teddy's octahedron is analogous to the bottom triangular face, which may be thought of as a rectified triangle (octahedron = rectified tetrahedron), and Teddy's bottom 4 tetrahedra is analogous to the 3 lateral triangles around this bottom triangular face. Teddy's tridiminished icosahedra are thus analogous to the pentagons of the tridiminished icosahedron.
The analogy can be taken further, in the sense that in 3D, an alternative construction of the tridiminished icosahedron is to start not from an icosahedron, but from a truncated tetrahedron, then shrink its bottom hexagonal face into a triangle (i.e., rectify it). This pulls the 3 surrounding triangles together to share vertices and turns the other 3 hexagons into pentagons. Teddy can similarly be constructed from the truncated 5-cell, by shrinking the hexagonal faces of the bottom truncated tetrahedron so that it turns into an octahedron (a sort of modified rectification). This pulls the 4 surrounding tetrahedra together, and causes the other 4 truncated tetrahedra to undergo a transformation into tridiminished icosahedra (one hexagon gets shrunk into a triangle, the other 3 hexagons turn into pentagons) -- analogous with how in 3D the hexagons transform into pentagons.
I have this suspicion that this construction is general, and there should be an analogous construction in 5D where you'll end up with a 5D polyteron consisting of 1 5-cell on top, 5 5-cells surrounding a rectified 5-cell at the bottom, with 5 Teddy's around the side. Topologically, at least, this construction is valid, but I'm not 100% sure it will be CRF, because the edge lengths and diteral angles may not line up correctly. If this shape is indeed a valid 5D CRF, then I shall have to call it the Grand Teddy, and if there's a CRF 6D analogue, then it will have to be the Great Grand Teddy. And it's Teddies all the way up! (You may groan now.)
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Quickfur's renders
quickfur wrote:If you can do cross-eyed viewing, the 3D shape of the projection should be even more helpful.
Oh come on, I'm practically the pioneer of cross-eyed viewing around here, didn't you know that?

It consists of 4 tridiminished icosahedra in tetrahedral formation, arranged around the top cell which is a tetrahedron, and at the bottom is an octahedron with 4 tetrahedra filling in the gaps between the bases of the tridiminished icosahedra. A really cute little shape. Teddy.
Well, these images suddenly made me realise something. The tridiminished icosahedron is in fact a member of an infinite family of polyhedra related to another family I'd been studying a while ago - the n-gonal trapezosemipyramids. The only difference is that in the latter family, the bottom face is not present, instead the triangles that would connect to it extend to a point to form kites. However, looking at the tridiminished icosahedron now, I see it is a type of antiprism, just with pentagons instead of the top set of triangles. So I'd like to call it the trigonal something-antiprism, which would make your "Teddy" the pentachoric (or pyrochoric) something-antiprism. Just a matter of figuring out what the something is, then you have my preferred name for it.
EDIT: Actually, seeing as the bottom cell in the "Teddy" is an octahedron, it's closer to the cupolae and rotundae than it is to the antiprisms. Perhaps we could just come up with another word in that vein?
I didn't count the edges myself; I got 216 edges from the convex hull algorithm that I use to construct the model that my viewer uses to do the projection. I don't know what went wrong with your edge count calculations, it seems reasonable to me. But counting things in higher-dimensional polytopes has always been a tricky business. I mean, I have enough trouble with counting elements correctly in 3D polyhedra, let alone 4D.
Is there any chance you could put something into your program to identify groups of transitive edges (or, more generally, elements of each dimension) and list those groups with the counts and number of cells surrounding them? This would likely help find the problem.
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Quickfur's renders
Keiji wrote:quickfur wrote:If you can do cross-eyed viewing, the 3D shape of the projection should be even more helpful.
Oh come on, I'm practically the pioneer of cross-eyed viewing around here, didn't you know that?
Really? Heh, I must've missed that.
 Either that, or my memory really is deteriorating with age.
Either that, or my memory really is deteriorating with age.[...] Well, these images suddenly made me realise something. The tridiminished icosahedron is in fact a member of an infinite family of polyhedra related to another family I'd been studying a while ago - the n-gonal trapezosemipyramids. The only difference is that in the latter family, the bottom face is not present, instead the triangles that would connect to it extend to a point to form kites. However, looking at the tridiminished icosahedron now, I see it is a type of antiprism, just with pentagons instead of the top set of triangles. So I'd like to call it the trigonal something-antiprism, which would make your "Teddy" the pentachoric (or pyrochoric) something-antiprism. Just a matter of figuring out what the something is, then you have my preferred name for it.
EDIT: Actually, seeing as the bottom cell in the "Teddy" is an octahedron, it's closer to the cupolae and rotundae than it is to the antiprisms. Perhaps we could just come up with another word in that vein?
Hmm. Based on the images I rendered in this post for the icosahedral version of Teddy, esp. the second pair of side-view images, I'd say that these shapes are a kind of truncated frustum. The tridiminished icosahedron, for example, can be thought of as a triangular frustum with its base corners cut off. Well, it's sortof a recti-truncation, because the base polygon gets rectified but the side polygons only get truncated. But the overall shape is a kind of frustum.
So maybe Teddy can be a tetrahedral truncated frustum? I'm not 100% happy with that name yet, though it's certainly more pronunciable than Wendy's notation for it.
 (Still, one has to admit that you can't beat Wendy's notation for precision.)
(Still, one has to admit that you can't beat Wendy's notation for precision.)I didn't count the edges myself; I got 216 edges from the convex hull algorithm that I use to construct the model that my viewer uses to do the projection. I don't know what went wrong with your edge count calculations, it seems reasonable to me. But counting things in higher-dimensional polytopes has always been a tricky business. I mean, I have enough trouble with counting elements correctly in 3D polyhedra, let alone 4D.
Is there any chance you could put something into your program to identify groups of transitive edges (or, more generally, elements of each dimension) and list those groups with the counts and number of cells surrounding them? This would likely help find the problem.
Transitivity checking is kinda hard to implement.
 But I did add a new command for classifying polytope elements based on how many ancestor elements (i.e. elements that contain them) they have. So here's a transcript of a calculation I did:
But I did add a new command for classifying polytope elements based on how many ancestor elements (i.e. elements that contain them) they have. So here's a transcript of a calculation I did:- Code: Select all
$ ./polyview -p data/crf/bi24dim600cell.def
Polytope bi_icositetradim_600cell loaded
Dimension: 4
72 vertices
216 edges
192 faces
48 cells
bi_icositetradim_600cell> calculate cell neighbours of edges
144 edges with 3 cells: all except 0, 2, 7, 10, 15-16, 18, 20, 25-26, 28-29, 37, 39-40, 46, 48-49, 51, 57, 59, 63, 68-69, 71, 73, 75, 77, 81, 88, 90-91, 97, 101, 104, 108, 111, 113, 117-118, 124, 126, 132-133, 138-139, 144, 149-151, 158-159, 161, 165, 168, 171, 176-177, 181, 183, 188, 190-192, 196-197, 199, 203-204, 207, 209, 212
72 edges with 4 cells: 0, 2, 7, 10, 15-16, 18, 20, 25-26, 28-29, 37, 39-40, 46, 48-49, 51, 57, 59, 63, 68-69, 71, 73, 75, 77, 81, 88, 90-91, 97, 101, 104, 108, 111, 113, 117-118, 124, 126, 132-133, 138-139, 144, 149-151, 158-159, 161, 165, 168, 171, 176-177, 181, 183, 188, 190-192, 196-197, 199, 203-204, 207, 209, 212
bi_icositetradim_600cell>
So there are 144 edges surrounded by 3 cells, and 72 edges surrounded by 4 cells. Unfortunately this doesn't tell us which part of the cells touch the edge. For that, maybe I can further refine the classification by distinguishing between parent elements of varying vertex counts? (The program can't easily tell what an element's global shape is, at the moment.)
- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Quickfur's renders
quickfur wrote:I have this suspicion that this construction is general, and there should be an analogous construction in 5D where you'll end up with a 5D polyteron consisting of 1 5-cell on top, 5 5-cells surrounding a rectified 5-cell at the bottom, with 5 Teddy's around the side. Topologically, at least, this construction is valid, but I'm not 100% sure it will be CRF, because the edge lengths and diteral angles may not line up correctly. If this shape is indeed a valid 5D CRF, then I shall have to call it the Grand Teddy, and if there's a CRF 6D analogue, then it will have to be the Great Grand Teddy. And it's Teddies all the way up! (You may groan now.)
Well, "teddi" is the Bowers acronym for the tridiminished icosahedron. Even so "Teddy" has a slightly different spelling, its direct application onto its 4d counterpart seems missleading and confusing. I would prefer "Teddy" just being a petname for "teddi" itself. Yesterday I suggested the 4d fellow to be called a "4d Teddy", note the slight difference.
As to "Teddies all the way up", yep, thats true. This is just Wendys sequence:
xfo&#xt > xfo3oox&#xt > xfo3oox3ooo&#xt > xfo3oox3ooo3ooo&#xt > ...
I never have verified whether those are possible without a kink at the middle layer, so.
But I dont see what could go wrong here.
The same holds true for the xfo3oox4ooo&#xt you doubted to be valid:
there the bottom figure is an oct. Onto its faces teddis are attached and folded up to connect at their pentagons. This partial complex is fully valid. And even the tips of those pentagons would connect (as faces are planar). The top faces of those teddis are triangles again, but anti-aligned to the bottom ones. In that very case there are 4 teddies symmetrically around every lower lacing edge of those teddis. Accordingly there emanate 4 triangles from this upper lacing edge vertex onto those anti-aligned top-face triangles. And as those top-face triangels are connected tip-wise (teddis do connect at the pentagons), the remaining space can be filled by squippies, and all then be completed by that final base, a co.
(Note that this o3x4o has its triangles truely ant-aligned to the triangles of the opposite layer, the x3o4o!)
Therefore I suppose you got some calculation error somewhere...
--- rk
- Klitzing
- Pentonian
- Posts: 1638
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Omnitruncated 24-cell
quickfur wrote:wendy wrote:You can of course derive snubs by alternating the vertices of a omnitruncate.
Yes, I understand that it is a general operation that works for any polytope (since an omnitruncate is always even).
You not even are restricted to even faces. You just have to apply alternation on a local level, and doing so then running around the original polytope. If that one somewhere has a odd face, you accordingly will have to run twice around the original polytope in order to come back to the beginning place with the same parity. - This is what Norman has contributed to snubbing theory, and what he calls a holosnub.
The snub-faces form by the removal of alternate vertices = "diminishing", which typically form simplexes. The degrees of freedom correspond to the number of dimensions (ie the marked dots in the dynkin graph), while the variables to set correspond to the edges of the triangle thus formed. When N=4, E=6, so you are attempting to solve four variables in six equations.
None the same, you can make vertices "the same" in symmetry, and one has to reckon only those edges which link different vertices, eg consider the {3,3,3}, where nodes become a3b3B3A. You have vertices types a=A, b=B,and edge types aA, bB, and aB=Ba. This is three variables in two unknowns, which is usually not solved. This is a shame, because the faces of this creature consist of ten icosahedra, twenty octahedra, and sixty tetrahedra, but only topological.
I'm more interested in actual uniform snubs, though. What is the general approach for deriving the coordinates of, say, the uniform snub cube? And for polytopes that do not have uniform snubs, is there a way to derive the "most symmetric" form of the snub generated by the alternation of its omnitruncate?
Yes, there is a gap between the application of an alternated facetting (which is applicable always) and its afterward topological deformation towards an uniform variant (which depends mainly on the degrees of freedom, but also, esp. when applied to starry forms, where the "edges underneath" get rather small, become zero or get retrograde, the "uniformisation", even if possible, becomes umbiguous). Cf. the corresponding outline within my article on that topic: "Snubs, Alternated Facetings, and Stott-Coxeter-Dynkin Diagrams", by Dr. R. Klitzing, Symmetry: Culture and Science, vol. 21, no.4, 329-344, 2010
(pdf available at http://bendwavy.org/klitzing/pdf/Stott_v8.pdf.
You can alternate some of the vertices, as long as an even (or unmarked = 2), branch connects marked and unmarked vertices. This gives,
s3s3s4o = s3s4o3o = snub 24choron, s4o3o3o = x3o3o4o.
You can apply stott-style addition to these things too, which gives the rather interesting, although not uniform s3s4o3x. The faces of this figure consist of 24 truncated tetrahedra, 24 icosahedra, and 96 triangular cupola (cuboctahedra cut across a hexagon). Allowing for non-uniform faces, one can have the equalateral figure formed by 3xo*xx2%o, or, as Richard Klitzing writes, cube || icosahedorn. This is a lace-prism, formed by a parallel planes containing a cube and an icosahedron, with assorted triangular prisms, tetrahedra, and square pyramids forming the lacing faces.
Yep, this type of alternated faceting with respect to other elements then vertices only was invented by myself, hehe. It translates completely into the Dynkin symbol description, then getting symbols containing "s"/"ß" (snub- resp. holosnub nodes), potentially "o" (unringed nodes), and "x" (ringed nodes). - An outline of that theory can be found as well in the mentioned article. In fact it was one of the reasons being written/published.
This is interesting; recently on Wikipedia somebody came up with 4D cupolas which are generated by expanding (runcinating) 4D pyramids.
Hmmm. There are different possible extrapolations of 3d concepts into 4d. Not only with respect to Johnson solids, leading either to the Blind polychora or to the CRFs, but even in what to call a 4d antiprism, and, what is relevant here, a cupola. I had outlined this within my original paper on segmentochora, starting at the bottom of page 6 of http://bendwavy.org/klitzing/pdf/artConvSeg_7.pdf. There too are arguments provided why to use them in the way I did - which contradict the usage you cited!
I wonder how many Johnson polychora there are, whose facets, to retain consistency with the generalization of the Archimedean polyhedra, are allowed to be any Johnson solid.
In particular, I'm quite curious as to whether there are vertex-transitive polytopes whose facets are not uniform (this is a possibility, e.g., if you take a Johnson solid whose vertices aren't transitive, say they are of two types X and Y, you can, when forming the polychoron, join the type X vertices of one facet with the type Y vertices of another, and thereby make the result vertex transitive---at least, this is why I think it may be possible, but I don't know if there are actual examples of such polytopes).
Hehe, there are such special thingies. Those are called scaliform polychora (formerly negatively being attributed as weakly uniform ones). Scaliform polychora are allowed to use Johnson solids for faces, yet require to be vertex transitive in their overall symmetry.
To provide an example consider prissi (http://bendwavy.org/klitzing/incmats/prissi.htm), which uses ikes, trips, tuts, and tricues for facets. (That one occured within my alternated faceting research. It indeed can be deformed to have unit edges throughout.)
An other example is the segmentochoron tut || inv tut (http://bendwavy.org/klitzing/incmats/tut=invtut.htm). That one has tuts, tets, and tricues for facets.
--- rk
- Klitzing
- Pentonian
- Posts: 1638
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Who is online
Users browsing this forum: No registered users and 25 guests
