Question regarding the real projective plane
20 posts
• Page 1 of 1
Question regarding the real projective plane
Looking into the wiki, wikipedia and other online resources, the immersions I could get for the real projective plane (RP2) are either a cross cap, roman surface, steiner surface, hemisphere with antipodalpoints identified or the boy's surface.
The first 3 get me confused as I 've no idea where I end up after passing the intersecting portions.
The boy's surface does not give the result indicated by the glue diagram of the RP2 (i.e. A moebius strip can be formed when I 'ant walked' in one direction but a tangle of bands which met with the original band in the wrong place when I 'ant walked' in the direction perpendicular to the first one (This is done by using a boy's surface model found in the online 3D warehouse, downloading the model into sketchup and then paint the sufaces one by one)).
I'm trying to piece the equator of the hemisphere representation together but so far unsuccessful.
Therefore my question is: What kind of maths is required to study the geometry of the RP2?
Because I want to see if it is possible to create an immersion that does not have pinch points like the cross cap, nor the confusing triple point present on the boy's surface, but rather a large region of intersection similar to the one found in the klein bottle immersion. (The intersection similar to that in the klein bottle immersion is so far the only thing i manage to visualize properly in 4D)
The first 3 get me confused as I 've no idea where I end up after passing the intersecting portions.
The boy's surface does not give the result indicated by the glue diagram of the RP2 (i.e. A moebius strip can be formed when I 'ant walked' in one direction but a tangle of bands which met with the original band in the wrong place when I 'ant walked' in the direction perpendicular to the first one (This is done by using a boy's surface model found in the online 3D warehouse, downloading the model into sketchup and then paint the sufaces one by one)).
I'm trying to piece the equator of the hemisphere representation together but so far unsuccessful.
Therefore my question is: What kind of maths is required to study the geometry of the RP2?
Because I want to see if it is possible to create an immersion that does not have pinch points like the cross cap, nor the confusing triple point present on the boy's surface, but rather a large region of intersection similar to the one found in the klein bottle immersion. (The intersection similar to that in the klein bottle immersion is so far the only thing i manage to visualize properly in 4D)
- Secret
- Trionian
- Posts: 162
- Joined: Tue Jul 06, 2010 12:03 pm
Re: Question regarding the real projective plane
I'm trying to piece the equator of the hemisphere representation together but so far unsuccessful.
Well, there's a reason for that - RP2 doesn't have an equator...
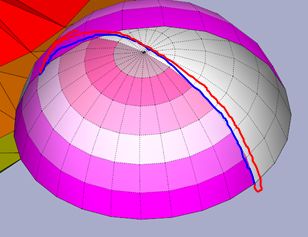
The following diagram (which I made, using this picture of yours as a reference in fact!) illustrates the hemisphere representation fairly accurately:
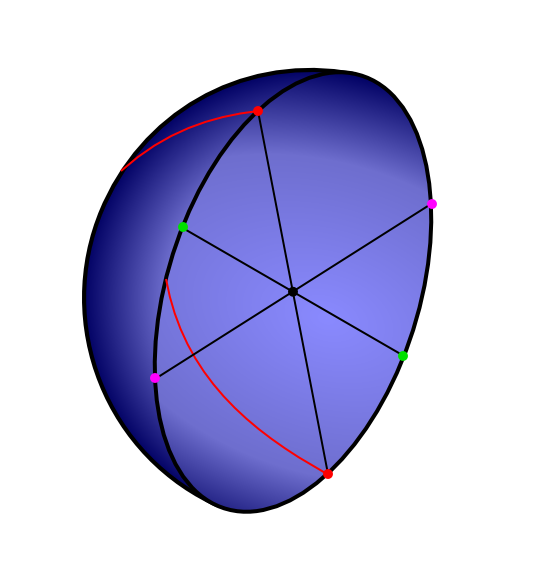
It is said the surface consists of the hemisphere with antipodal points identified.
What this means is that every point on the circular boundary is, in the surface, the exact same point as the point 180 degrees opposite from it on that circle.
I've exemplified with my pairs of red, green and pink points connected by the black lines. We see two points of each color, but each pair is actually only one single point.
The red curve shows a path drawn inside the surface. It begins somewhere on the outside of the hemisphere, travels up and to the right (from our POV) to the top red point. It then "jumps" to the bottom red point (from our POV, that is - on the surface itself, the distance of this "jump" is zero) and continues on the inside of the hemisphere.
If you imagine the curve is moved slightly so that the bit on the outside "joins up" with the bit on the inside by "switching sides", you can see it's quite analogous to a loop around a Moebius strip.
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Question regarding the real projective plane
Keiji wrote:http://teamikaria.com/hddb/dl/FHEVA987RR8ZM8SBEXEYC18QJY.png[/url]
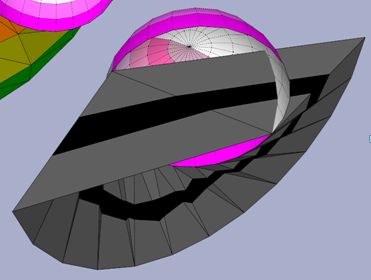
Using this image, I made something like this as an attempt to seal the opening

Here I manage to connect the ends so that an ant walk of the above object will produce the result as indicated in your illustration (i.e. both 'inside' and 'outside' of the hemisphere are connected).
The problem is: The whole thing is 3D with no self intersection and more importantly, there's still an inside and outside.
For it to be an real projective plane, does it required to be non orientable no matter which way you walk? (because from internet I discovered that the klein bottle actually have two bands that are orientable)
- Secret
- Trionian
- Posts: 162
- Joined: Tue Jul 06, 2010 12:03 pm
Re: Question regarding the real projective plane
I'm not sure what that image is supposed to represent, but it certainly doesn't look like I expect an RP2 to.
Yes, there needs to be only one side. If it has a distinct inside and outside it's definitely not RP2.
Well, on any surface orientable or not, you can walk in a circle and get back to where you started without flipping sides. On RP2 for example, just look at my diagram and imagine drawing a circle anywhere on the surface of the hemisphere without touching the black boundary circle. As you can see, it appears to be "locally orientable" - as do all surfaces.
Yes, there needs to be only one side. If it has a distinct inside and outside it's definitely not RP2.
Secret wrote:does it required to be non orientable no matter which way you walk?
Well, on any surface orientable or not, you can walk in a circle and get back to where you started without flipping sides. On RP2 for example, just look at my diagram and imagine drawing a circle anywhere on the surface of the hemisphere without touching the black boundary circle. As you can see, it appears to be "locally orientable" - as do all surfaces.
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Question regarding the real projective plane
Keiji wrote: As you can see, it appears to be "locally orientable" - as do all surfaces.
Thanks!
I thought non orientable shapes are non orientable even if you walk in mini circles
Currently working on another RP2 illustration proposal, will post it here later
P.S. Is it mathematically possible to have a RP2 immersion with huge kelin bottle like self intersecting regions instead of points? (i.e. 4D twist regions)
EDIT: AT LAST, 5 weeks of paperwork and sleepless nights had finally paid off. If that is it, I can finally get some good rest


Color bands indicate 'ant walk tests' done on the surface
Ran through all sections, including the middle 'messy region' (which in the recent paper work I've forced it into a singularity, but finally managed to get through it)
Below is the googlesketchup file for detailed verification
https://docs.google.com/leaf?id=0B11-z8yC5qelZDJmNWIxZTAtNjBkYy00OTZjLWE0ZGQtNDY0ZmQwZDdjNmFi&hl=zh_TW&authkey=CNWph5gP
If this is verified to be (one of the possible) projections of RP2. Then this is the first ever immersion that have no pinch points nor the confusing triple point of the boy's surface. And it'll be easy to track how the non orientable bits forms on the surface.
- Secret
- Trionian
- Posts: 162
- Joined: Tue Jul 06, 2010 12:03 pm
Re: Question regarding the real projective plane
Well, this almost works - unfortunately, you can't just get rid of the "pinch points" like that.
It works fine to take, say, your red/green band from the "far" side of the hemisphere, and stretch it up, over and around to meet the near side. You can then make that band bigger and bigger, until almost all of the circle is covered. But you can't have it touch the "equatorial" points: suppose you stretch the band out from one of the equatorial points (which is of course the same point as the other, as far as the surface itself is concerned), then you will eventually reach the other point... but wait, that point has already been stretched out because it's the same point! So you need to stretch further to reach where you are trying to get to, and you will end up stretching it forever, never reaching the destination, like a dog chasing its own tail - unless you let yourself create a pinch point, which lets you get there.
As a simple reason why your diagram isn't accurate, notice you've stretched out the equatorial point(s) into not just a line, but a plane. You'd have to collapse that into a line, giving you something that looked like a mutilated torus, and then into a point, to get an accurate immersion, which would probably give you one of the immersions we already know of.
It works fine to take, say, your red/green band from the "far" side of the hemisphere, and stretch it up, over and around to meet the near side. You can then make that band bigger and bigger, until almost all of the circle is covered. But you can't have it touch the "equatorial" points: suppose you stretch the band out from one of the equatorial points (which is of course the same point as the other, as far as the surface itself is concerned), then you will eventually reach the other point... but wait, that point has already been stretched out because it's the same point! So you need to stretch further to reach where you are trying to get to, and you will end up stretching it forever, never reaching the destination, like a dog chasing its own tail - unless you let yourself create a pinch point, which lets you get there.
As a simple reason why your diagram isn't accurate, notice you've stretched out the equatorial point(s) into not just a line, but a plane. You'd have to collapse that into a line, giving you something that looked like a mutilated torus, and then into a point, to get an accurate immersion, which would probably give you one of the immersions we already know of.
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Question regarding the real projective plane
You may find this helpful:
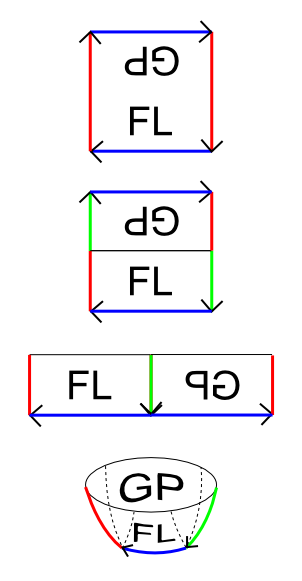
The first image shows the fundamental polygon of the RP2, with some letters in it to help show how parts get moved around (there's no significance to the letters, they're just nice asymmetrical symbols). We know the square must be folded up with blue arrows connected to each other, and similarly for red, with arrowheads lining up.
Let's pretend we're going to make a circular cut through the RP2. This can just as easily be done by making a cut through the fundamental polygon instead and then connecting it up as usual, so in the second image I've drawn a line in the middle where we're cutting. I've also split the red edge(s) in halves, introducing a green "half-edge" as well as the remaining red half-edge.
In the third image, we've actually done the cut, and have stuck the green half-edges together. This leaves the red half-edge and blue edge to glue. It should be fairly obvious that doing this produces the hemisphere shown in the fourth image.
By looking at the letters, and asking what happens when you go "up" from any letter, you can see easily that the antipodal points along the circular boundary are identified and it's clear that this is a valid representation of RP2.

The first image shows the fundamental polygon of the RP2, with some letters in it to help show how parts get moved around (there's no significance to the letters, they're just nice asymmetrical symbols). We know the square must be folded up with blue arrows connected to each other, and similarly for red, with arrowheads lining up.
Let's pretend we're going to make a circular cut through the RP2. This can just as easily be done by making a cut through the fundamental polygon instead and then connecting it up as usual, so in the second image I've drawn a line in the middle where we're cutting. I've also split the red edge(s) in halves, introducing a green "half-edge" as well as the remaining red half-edge.
In the third image, we've actually done the cut, and have stuck the green half-edges together. This leaves the red half-edge and blue edge to glue. It should be fairly obvious that doing this produces the hemisphere shown in the fourth image.
By looking at the letters, and asking what happens when you go "up" from any letter, you can see easily that the antipodal points along the circular boundary are identified and it's clear that this is a valid representation of RP2.
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Question regarding the real projective plane
Keiji wrote:You'd have to collapse that into a line, giving you something that looked like a mutilated torus, and then into a point, to get an accurate immersion, which would probably give you one of the immersions we already know of.
here's the resulted object after doing the above instructions

https://docs.google.com/leaf?id=0B11-z8yC5qelNGMyOWFlMjAtN2RhNy00YjkyLTljMjUtZWU0ZTZlMTk1MTU0&hl=zh_TW&authkey=CIvK-uEI (For the 3D model)
And in response to the fundamental polygon post:
Yup I understand how the sides are connected.
Myabe I'm a really stubbon visual person, but the reason why I'm not satisfied with the hemisphere representation is that the circular boundary remains unglued in the image. Because it is unglued, it looks incomplete. To me, even though I understand how they switch sides and connect as illustrated, it looks as if it 'magically' jumped from one end to another. The RP2 doesn't look like a 'closed surface' (layman) in the hemisphere representation (as there's clearly an opening visible in the representation)
But for the immersion of the klein bottle, It is completely glued. Even though there's a self intersection (which looks weird for laymans), I think laymans will agree that it is a 'closed surface' after looking at it.
Looking at the various immersions out there in the internet does not help much as they always have pointed regions (pinch points of the cross cap, roman surface, steiner surface, and the triple point in the boy's surface).
Both RP2 and Klein bottle can be placed/embebbed in 4D space without self intersections.
For the klein bottle, the intersection is a broad region, and the region where the 4D twist takes place is easily visible(In 3D model for most people, and on 2D drawings for some)
With suffieint training in 4D interpertations, one can easily see it without the self intersection.
But for the RP2, the presence of pointed regions make it really difficult to do 'ant walks' properly. (Maybe it's just me) it looks weird when you get to the pinch point, you switch sides, with no signs of twist visible, unlike the klein bottle and the moebius strip (cross cap and other immersions)
For the boy's surface. (Maybe it's just me who don't understand its geometry) the 4D twist is obsurbed by 3 planar portions which all intersects at one point (the triple point).
In 4D interpretations, I just don't understand how the portions near the pointed region are far apart from each other (Unlike the klein bottle)
Seeing that nearly all immersions contains point intersection, is the RP2 actually pointed even in 4D?
Or is it mathematically impossible to have RP2 immersions without point intersections?
(In case you wonder why I still ask this question: The ans to this can tell me whether i should continue to pusurade that elusive immersion. Because if that is true but I manage to make that immersion, that means maths (at least in this context) is false. But I think this is very unlikely, thus I'll stop looking for that immersion if the ans to the question is true(and leave it until I got to uni))
- Secret
- Trionian
- Posts: 162
- Joined: Tue Jul 06, 2010 12:03 pm
Re: Question regarding the real projective plane
Secret wrote:Keiji wrote:You'd have to collapse that into a line, giving you something that looked like a mutilated torus, and then into a point, to get an accurate immersion, which would probably give you one of the immersions we already know of.
here's the resulted object after doing the above instructions
https://docs.google.com/leaf?id=0B11-z8yC5qelNGMyOWFlMjAtN2RhNy00YjkyLTljMjUtZWU0ZTZlMTk1MTU0&hl=zh_TW&authkey=CIvK-uEI (For the 3D model)
I'm pretty sure the 2nd object across is correct: you've collapsed the plane into a circle in the first version, and then into a point in the second as required - any further collapsing isn't necessary (and would make it not the RP2 again). It would be nice if someone else could come here and verify this though, I could be wrong.
Secret wrote:Myabe I'm a really stubbon visual person, but the reason why I'm not satisfied with the hemisphere representation is that the circular boundary remains unglued in the image. Because it is unglued, it looks incomplete. To me, even though I understand how they switch sides and connect as illustrated, it looks as if it 'magically' jumped from one end to another. The RP2 doesn't look like a 'closed surface' (layman) in the hemisphere representation (as there's clearly an opening visible in the representation)
Yeah, I know what you mean and I agree with you. I've never been able to properly visualize RP2 myself either, which is the main reason I'm interested in this thread.

I think the Boy's surface is actually the easiest to understand, though the animation on Wikipedia is not particularly useful by itself as it rotates far too fast through the crucial moments. I downloaded it and loaded it in GIMP to go through each frame at a time though, and by doing this I managed to find the loop of interest:
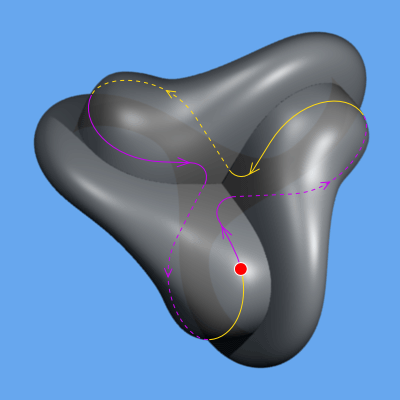
Starting at the red dot and following the arrows, we flip orientation between purple and yellow once per lobe, and travel through three lobes to return to the red dot. Thus, by the time we get back where we started, we've flipped orientation three times, which is odd, showing the surface is non-orientable. So while the C3 symmetry might seem unintuitive for a manifold that was constructed from a square (with D8 symmetry), it is actually what allows us to derive non-orientability.
Notice that even though this non-orientable loop cannot be shrunk to a point while staying inside the loop, if we draw any orientable loop, it can be shrunk to a point, showing that this manifold has zero genus. Now it has been proven that any non-orientable 2-manifold with zero genus is equivalent to RP2, so this tells us that Boy's surface must be RP2.
Secret wrote:Seeing that nearly all immersions contains point intersection, is the RP2 actually pointed even in 4D?
Or is it mathematically impossible to have RP2 immersions without point intersections?
(In case you wonder why I still ask this question: The ans to this can tell me whether i should continue to pusurade that elusive immersion. Because if that is true but I manage to make that immersion, that means maths (at least in this context) is false. But I think this is very unlikely, thus I'll stop looking for that immersion if the ans to the question is true(and leave it until I got to uni))
Do note, there's nothing "pointy" about RP2 - only that it happens to contain a point where three disconnected regions of the plane intersect (as in Boy's surface) or a point where a circular sweeping section has been inverted (as in the second variation of your latest rendering that I verified above).
If you picture in the realm (three-dimensional space) two perpendicular planes, you'll see they intersect at a line. If you replace one of those planes with an (infinite, uncapped) cylinder, you get a circular intersection, which is what happens in the Klein bottle. But if you look at three perpendicular planes, they will intersect at a point, and no matter how you move, rotate, or deform the planes, they'll always intersect in one point. Similarly to how you can't find a way to have three perpendicular planes which don't intersect at a point, you also can't find an immersion of RP2 without such a point.
For a more convincing demonstration, consider the following facts:
Sphere - genus 0, orientable (0S)
Torus - genus 1, orientable (1S)
RP2 - genus 0, non-orientable (0A)
Klein bottle - genus 1, orientable (1A)
If you take the Klein bottle and pull it "taut" to get rid of the circle of self-intersection, what you end up with is a torus with a pinch point where the circular sweeping section inverts. Of course, if you then disconnect it from itself, rotate 180 degrees and re-connect, you get the normal torus, and this has kept the genus the same (one) but made the surface orientable, or in short we've gone from 1A to 1S. Similarly, we can go backwards from 1S to 1A.
Now, if we can go 1A to 1S and back, why can't we do the same for 0A and 0S? Well, part of what we did involved pulling the thing taut - we needed a hole to do that, and the only way to have a hole is to have a genus of (at least) 1. So while the conversion between a pinch point and circular self-intersection works when you have genus 1, you can see it doesn't work for genus 0, so the non-orientability must come from a pinch point.
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Question regarding the real projective plane
In respond to the boy's surface:
For what I know about ant walks, you only walk striaght forward (locally) on the surface. Therefore on the pic where you approches the lobes and suddenly make a 90o turn into the lobe looks weird to me (as you supposed to go straight forward into another lobe nearby). And that's why I haven't considered this path.
(Using boy's surface model found in the 3D warehouse (because I don't know how to make such a thing with complicated curves in the perspective of sketchup) and do ant walks as mentioned above results a curve which connect with the correct sides, but connected midway to the original curve (i.e. in the wrong ends!))
So my question is: Is the 'ant' not allowed to (locally) change directions?
Ah, now I know how they prove it.
Hmm in that case, it seems boy's surface is the only one with the twist most visible. So I think I should try to work out a RP2 immersion that is similar to boy's surface but not a convoluted as it, that way I might be easier to see how RP2 will look like in 4D based on the knowledge learnt from the klein bottle.
Btw if I understand your "3 perpendicular plane theory" correctly, does that mean RP2 self intersect/the planes touches at a point even in 4D?
Do you mean the blue circle here is a pinch point?

Hmm so that means we've to understand how sides are switched at the pinch points, or the geometry of boy's surface in order to visualize RP2 properly.
BTW here's a condensed version of my 2nd render

https://docs.google.com/leaf?id=0B11-z8yC5qelYzlkN2MxZjItYWMyMC00ZmFlLWFjOTYtZGQwMGNhN2E3ZGRm&hl=zh_TW&authkey=CLuupKsJ
(Inculde a question in the pic)
The middle spherical representation looks quite simple except for that twisting band that sticks onto it. Suprisingly, the twist is done near the interface between the upper rim of the spherical horn torus and the twisting band instead of in the middle of the band. Another twist is done at the pinch point of the horn torus portion.
And a recent search on the internet gives me this:

(There are more of these out there, I also found one made of 5 klein bottles fused together, but these are rare compared to the more well known immersions)
I don't think this is homomorphic to the boy's surface as one only finds a single band of non orientable loop when walking in one direction but a series of orientable loops if one walks within the neck of the klein bottles
One can adjust the 'width' of the klein bottles so that they cannot interset at one point
But if this is really homomorphic to boy's surface, then (insert suitable words here) ...
For what I know about ant walks, you only walk striaght forward (locally) on the surface. Therefore on the pic where you approches the lobes and suddenly make a 90o turn into the lobe looks weird to me (as you supposed to go straight forward into another lobe nearby). And that's why I haven't considered this path.
(Using boy's surface model found in the 3D warehouse (because I don't know how to make such a thing with complicated curves in the perspective of sketchup) and do ant walks as mentioned above results a curve which connect with the correct sides, but connected midway to the original curve (i.e. in the wrong ends!))
So my question is: Is the 'ant' not allowed to (locally) change directions?
Keiji wrote:[...]so this tells us that Boy's surface must be RP2.
Ah, now I know how they prove it.
Keiji wrote:Do note, there's nothing "pointy" about RP2 - only that it happens to contain a point where three disconnected regions of the plane intersect (as in Boy's surface) or a point where a circular sweeping section has been inverted (as in the second variation of your latest rendering that I verified above).
Similarly to how you can't find a way to have three perpendicular planes which don't intersect at a point, you also can't find an immersion of RP2 without such a point.
Hmm in that case, it seems boy's surface is the only one with the twist most visible. So I think I should try to work out a RP2 immersion that is similar to boy's surface but not a convoluted as it, that way I might be easier to see how RP2 will look like in 4D based on the knowledge learnt from the klein bottle.
Btw if I understand your "3 perpendicular plane theory" correctly, does that mean RP2 self intersect/the planes touches at a point even in 4D?
Keiji wrote:If you take the Klein bottle and pull it "taut" to get rid of the circle of self-intersection, what you end up with is a torus with a pinch point where the circular sweeping section inverts.[...]
Do you mean the blue circle here is a pinch point?

Keiji wrote:you can see it doesn't work for genus 0, so the non-orientability must come from a pinch point.
Hmm so that means we've to understand how sides are switched at the pinch points, or the geometry of boy's surface in order to visualize RP2 properly.
BTW here's a condensed version of my 2nd render

https://docs.google.com/leaf?id=0B11-z8yC5qelYzlkN2MxZjItYWMyMC00ZmFlLWFjOTYtZGQwMGNhN2E3ZGRm&hl=zh_TW&authkey=CLuupKsJ
(Inculde a question in the pic)
The middle spherical representation looks quite simple except for that twisting band that sticks onto it. Suprisingly, the twist is done near the interface between the upper rim of the spherical horn torus and the twisting band instead of in the middle of the band. Another twist is done at the pinch point of the horn torus portion.
And a recent search on the internet gives me this:

(There are more of these out there, I also found one made of 5 klein bottles fused together, but these are rare compared to the more well known immersions)
I don't think this is homomorphic to the boy's surface as one only finds a single band of non orientable loop when walking in one direction but a series of orientable loops if one walks within the neck of the klein bottles
One can adjust the 'width' of the klein bottles so that they cannot interset at one point
But if this is really homomorphic to boy's surface, then (insert suitable words here) ...
- Secret
- Trionian
- Posts: 162
- Joined: Tue Jul 06, 2010 12:03 pm
Re: Question regarding the real projective plane
Secret wrote:In respond to the boy's surface:
For what I know about ant walks, you only walk striaght forward (locally) on the surface. Therefore on the pic where you approches the lobes and suddenly make a 90o turn into the lobe looks weird to me (as you supposed to go straight forward into another lobe nearby). And that's why I haven't considered this path.
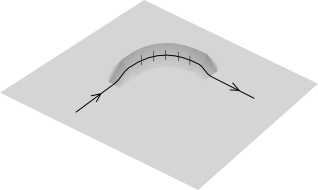
Well, yes, you are allowed to change directions. Simple reasoning is as follows: Consider turning 90 degrees (or whatever) in a curve on a flat plane. Now, look at your path, and deform the plane so that at each point in the curve of the path, the plane is oriented perpendicular to its original direction. This actually deforms the path which was a curve into a straight line - straight lines are acceptable, and the deformation we used was acceptable, so the original curved path is also acceptable. This is illustrated below:
Secret wrote:Btw if I understand your "3 perpendicular plane theory" correctly, does that mean RP2 self intersect/the planes touches at a point even in 4D?
No, they should not intersect in 4D. If you consider the 3 perpendicular planes in the realm, and add an extra dimension to obtain a flune (four-dimensional space), then of course those three planes would be completely flat in the fourth dimension. You can now move each of those planes by different amounts through the fourth dimension, and none will intersect. This is line having a number of intersecting lines in 2D, and then introducing a third dimension and "stacking" the lines so that none of them intersect any more. Just imagine strands of hay laying atop one another; no matter how many they are, they don't intersect (because that's impossible for physical objects, of course), even though they "cross over" each other when observed from above.
No. I was just now working on a diagram of a pinch point when unfortunately Inkscape froze and I'm not going to bother doing it all over again.
You can try it yourself, though. Take a cylinder, or more specifically take the circular ends of a cylinder and consider the lines between the ends. Slowly rotate one end around the axis through the cylinder, and watch what happens to the lines: they form a circle in the middle which shrinks smaller and smaller. Once you've rotated the end through exactly 180 degrees, that circle shrinks to a point. That is the pinch point.
Pinch points are points; a circle isn't a point. But the blue circle you mentioned does become a pinch point (by shrinking to it) if you pull the Klein bottle taut.
Don't really have time to investigate the remainder of your findings now, though that triple Klein bottle is certainly interesting though it looks quite suspicious, I wouldn't jump to saying it was RP2 just yet.
-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Question regarding the real projective plane
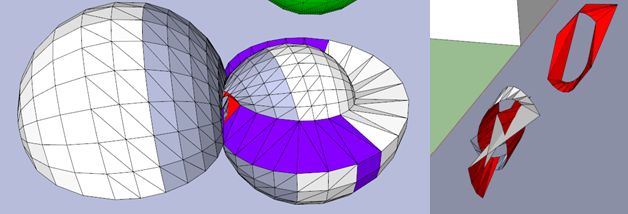
Another render, I'm not sure if it is RP2 (As it fails to pass the connected sum test), is it because I've done something illegal such as the 'dog chasing tail move?' (mind point where i did the illegal move, if any?)
https://docs.google.com/leaf?id=0B11-z8 ... y=CLCT87kJ (link to the 3D model)

(The above figure is made by 'folding' the fundamental polygon instead of the hemisphere that i usually used. I first glue the first pair of ends in the polygon into the moebius strip, then stretch one arm of the moebius strip and spin it to the other arm so they matches (with one point fixed in the process, presumably the pinch point))
I'm not sure about the triple klein bottle also
EDIT: the triple Klein bottle has a hole. Therefore any orientable loop around the cylindrical portions cannot be shrunk to a point. Therefore it is not RP2
https://docs.google.com/leaf?id=0B11-z8 ... y=CLCT87kJ (link to the 3D model)

(The above figure is made by 'folding' the fundamental polygon instead of the hemisphere that i usually used. I first glue the first pair of ends in the polygon into the moebius strip, then stretch one arm of the moebius strip and spin it to the other arm so they matches (with one point fixed in the process, presumably the pinch point))
EDIT: the triple Klein bottle has a hole. Therefore any orientable loop around the cylindrical portions cannot be shrunk to a point. Therefore it is not RP2
- Secret
- Trionian
- Posts: 162
- Joined: Tue Jul 06, 2010 12:03 pm
Re: Question regarding the real projective plane


https://docs.google.com/leaf?id=0B11-z8 ... y=CNzmraMK
This is the newest atempt of the real projective plane
so far it has passed the following tests:
1. Connected sum test
2. Non orientability test
3. genus 0 test

Illustration of the connected sum test.
This render is quite similar to the cross cap, having a (forgot name) umbrella like region in the projection model
This render is done by folding from a square piece of paper, using the knowledge of the klein bottle
What 's more need to be tested to ensure it is a valid representation of RP2?
- Secret
- Trionian
- Posts: 162
- Joined: Tue Jul 06, 2010 12:03 pm
Re: Question regarding the real projective plane
Looks good, I'll leave it to the others to prove that it's RP2 though, since I'm never confident of proving things 

-

Keiji - Administrator
- Posts: 1985
- Joined: Mon Nov 10, 2003 6:33 pm
- Location: Torquay, England
Re: Question regarding the real projective plane
The simplest smooth RP2 model that I know may be made of the half of the Klein Bottle. It is shown on this picture as a sequence of slices:
http://ompldr.org/vOTk1cg.png Mod edit: Do not post .bmp images, these waste user's time and bandwidth which may be expensive for some users. I have converted this to .png, please do so yourself in future. ~Keiji
Only one intersection point of the profiles is real - at the top of slice 4, it's a saddle point of the surface. Others are the results of embedding of RP2 in 3D. By different color the sequence of "circles" is shown, they go from some projective line (red) to the point (light grey). I think that existance of this sequence proves that it's really a projective plane.
But what the surface is it? I tried to draw it's 3D form, but failed (too many self-intersections). And I can't imagine Boy's surface to check if it's the same as my surface or not. May be somebody can recognize it?
http://ompldr.org/vOTk1cg.png Mod edit: Do not post .bmp images, these waste user's time and bandwidth which may be expensive for some users. I have converted this to .png, please do so yourself in future. ~Keiji
Only one intersection point of the profiles is real - at the top of slice 4, it's a saddle point of the surface. Others are the results of embedding of RP2 in 3D. By different color the sequence of "circles" is shown, they go from some projective line (red) to the point (light grey). I think that existance of this sequence proves that it's really a projective plane.
But what the surface is it? I tried to draw it's 3D form, but failed (too many self-intersections). And I can't imagine Boy's surface to check if it's the same as my surface or not. May be somebody can recognize it?
- Mrrl
- Trionian
- Posts: 165
- Joined: Sun May 29, 2011 7:37 am
Re: Question regarding the real projective plane
The real projective plane is a variation of geometry, which i gloss as mE.
The nature of geometry is in the first part, by the curvature of space, as E (0), S(+) and H(-). These correspond to the cone-sections of parabolic, elliptic and hyperbolic. The first letter is either f or o or m, according to which of the elements of this statement is rejected: "[in complete (f)], [orientable (m)] space two lines cross [once (o)]". Euclid describes fE, the fragment of euclidean space. Since spheric space exists, it is orientable, but lines cross twice, ie it's oS. Elliptic space corrects the single crossing for axiomic reasons, but causes it to be non-orientable: it's mS.
One supposes the existence of similar complete geometries for E and for H. The geometry derived from the artist's projections follow the general rule of mE, which means that it is non-orientable.
The non-orientable nature of the surface does not prevent it from being locally non-orientable, or that it is able to hold content. The out-vector can reverse over an 'askew marginoid', usually such occurs where surfaces cross. The density of the surface itself does not change, but the across-vector reverses.
A polyhedron, described on Bower's list as the Thah, is in the general shape of an octahedron, with four alternating triangles replaced by three diametric squares. The surface is closed, and a walk on it shows that it is generally non-orientable. However, it evidently contains as volume, the four octants that are of non-removed triangles. One supposes the existence of askew marginoids, which reverses the in/out vector, and the path that demonstrates such non-orientability crosses an odd number of these on the way back to the original point.
Something like the klein bottle, can exist without intersection in four dimensions, but it's not a surface: it's a hedrix, the thing is a kind of knot, not a kind of boundary. One could, i suppose, build it into a polytope, but the thing would have holes of various kinds, in much the same way that an a reef knot exists on the surface of a torus without intersection.
I usually hold the projective geometries to be an unproductive dead end, save for enumerating colour-groups. It's a limited version of real geometry. The nature of the projective plane, then is set by the presentation of the projective point 'u' (point defining straight lines).
In projective geometry, straight lines are straight lines, but the nature of the point u is either an ellipse (including a circle), or a straight line, or nothing, as the geometry is H or E or S respectively. Only in the Euclidean geometry is the infinite space represented by a straight line. But in the main, projective geometry is about alignments of straight lines, and it is only when the infinite is brought to bear on problem, that the geometry divides.
Some theroms, like the Desarges alignments, work in project geometry, and hence works in all three spaces.
But when one tries to realise a projective plane, of any kind, one is left with the realisation of 'u', variously as a "pencil of lines" through a centre of the circle (the projective S geometry), or a line of infinity (in the euclidean geometry), or the bounding conic (in the hyperbolic), which seeks to cause problems.
The nature of geometry is in the first part, by the curvature of space, as E (0), S(+) and H(-). These correspond to the cone-sections of parabolic, elliptic and hyperbolic. The first letter is either f or o or m, according to which of the elements of this statement is rejected: "[in complete (f)], [orientable (m)] space two lines cross [once (o)]". Euclid describes fE, the fragment of euclidean space. Since spheric space exists, it is orientable, but lines cross twice, ie it's oS. Elliptic space corrects the single crossing for axiomic reasons, but causes it to be non-orientable: it's mS.
One supposes the existence of similar complete geometries for E and for H. The geometry derived from the artist's projections follow the general rule of mE, which means that it is non-orientable.
The non-orientable nature of the surface does not prevent it from being locally non-orientable, or that it is able to hold content. The out-vector can reverse over an 'askew marginoid', usually such occurs where surfaces cross. The density of the surface itself does not change, but the across-vector reverses.
A polyhedron, described on Bower's list as the Thah, is in the general shape of an octahedron, with four alternating triangles replaced by three diametric squares. The surface is closed, and a walk on it shows that it is generally non-orientable. However, it evidently contains as volume, the four octants that are of non-removed triangles. One supposes the existence of askew marginoids, which reverses the in/out vector, and the path that demonstrates such non-orientability crosses an odd number of these on the way back to the original point.
Something like the klein bottle, can exist without intersection in four dimensions, but it's not a surface: it's a hedrix, the thing is a kind of knot, not a kind of boundary. One could, i suppose, build it into a polytope, but the thing would have holes of various kinds, in much the same way that an a reef knot exists on the surface of a torus without intersection.
I usually hold the projective geometries to be an unproductive dead end, save for enumerating colour-groups. It's a limited version of real geometry. The nature of the projective plane, then is set by the presentation of the projective point 'u' (point defining straight lines).
In projective geometry, straight lines are straight lines, but the nature of the point u is either an ellipse (including a circle), or a straight line, or nothing, as the geometry is H or E or S respectively. Only in the Euclidean geometry is the infinite space represented by a straight line. But in the main, projective geometry is about alignments of straight lines, and it is only when the infinite is brought to bear on problem, that the geometry divides.
Some theroms, like the Desarges alignments, work in project geometry, and hence works in all three spaces.
But when one tries to realise a projective plane, of any kind, one is left with the realisation of 'u', variously as a "pencil of lines" through a centre of the circle (the projective S geometry), or a line of infinity (in the euclidean geometry), or the bounding conic (in the hyperbolic), which seeks to cause problems.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2014
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Question regarding the real projective plane
wendy wrote:...[in complete (f)]...Since spheric space exists, it is orientable, but lines cross twice, ie it's oS. Elliptic space corrects the single crossing for axiomic reasons, but causes it to be non-orientable: it's mS...One supposes the existence of similar complete geometries for E and for H. The geometry derived from the artist's projections follow the general rule of mE, which means that it is non-orientable.
The only word here I don't understand is "in complete", I tried to look for this math element on google and your PG but found nothing.
I'm also wondering whether the common RP2 models out there (boy's surface, steiner surface, cross cap, roman surface and its polyhedral representation) are mE or mS or mH?
wendy wrote:...The out-vector can reverse over an 'askew marginoid', usually such occurs where surfaces cross. The density of the surface itself does not change, but the across-vector reverses.
Even after checking the PG, I'm still confused on what "density" is (tracing the meaning of "out vector" leads to "density" and "surtope", and then "density" to "flag" and finally "periform", which I fail to understand it).
For the description of out vector without considering the "density" part, can I say the out vector is a vector pointing from the inside of the polytope to the outside which perpendicular to the bounding surface (i.e. the surtopes)?
There are no entries on across vector, so I assume that is refer to "Transverse outvectors"
So if what I said above is correct, do you mean the vector is initially pointing 'outward' RP2, then when it approches the askew marginoid (which according to the PG I tried to interpret as the "margin" where inside and outside reverses) the vector becomes shorter and eventually becomes a zero vector (Interpreted from
) at the "askew marginoid", and then lengthen but with the direction now pointing 'inward' RP2 after passing through the "askew marginoid"?...there should be no net transverse outvector...
Also according to the description of "margins", in the case of RP2, that means there's a line that bounds the 2D surface of RP2. Is that the line at infinity, or did I misinterpret the meaning?
wendy wrote:...Thah...
A wikipedia search yields the Tetrahemihexahedron, which after reading that this paragraph becomes more understandable. However I'm still confused on the shape of the volume of this shape and the RP2 in general
wendy wrote:...One could, i suppose, build it into a polytope, but the thing would have holes of various kinds, in much the same way that an a reef knot exists on the surface of a torus without intersection...
Although I understand what a hedrix and a reef knot is, I'm still confused on how the reef knot is possible on the "2D surface of the torus" (torohedrix?) without intersection
wendy wrote:I usually hold the projective geometries to be an unproductive dead end...The nature of the projective plane, then is set by the presentation of the projective point 'u' (point defining straight lines).
For 1st part, the reason of trying to understand RP2 and 4D in general is merely of interest to visualise them. As I'ven't get to uni yet, I still yet to appreciate the maths behind these 4D shapes.
For 2nd part, do you mean RP2 is defined by striaght lines in E or S which appears as a point on RP2?
wendy wrote:...and it is only when the infinite is brought to bear on problem, that the geometry divides.
Do you mean:
Shape of point u
mS: Centre of circle/hyperspheres
mE: Line
mH: Ellipse
But for the rest of the properties (presence of odd number of askew marginoid, uniform density, a volume) remains unchanged in all 3 projective geometries?
wendy wrote:Some theroms, like the Desarges alignments, work in project geometry, and hence works in all three spaces.
Do you mean Desargues theorem?
wendy wrote:But when one tries to realise a projective plane, of any kind, one is left with the realisation of 'u', variously as a "pencil of lines" through a centre of the circle (the projective S geometry), or a line of infinity (in the euclidean geometry), or the bounding conic (in the hyperbolic), which seeks to cause problems.
I don't understand what the "problems" are...
==============================================
Also to sum up, does that means for a model to be RP2, there must be "an area present where inside and outside reverses (askew marginoid) when passes through and that there are no holes", only?
- Secret
- Trionian
- Posts: 162
- Joined: Tue Jul 06, 2010 12:03 pm
Re: Question regarding the real projective plane
DENSITY
When surfaces are allowed to cross, the solid nature of figures is replaced by the notion of 'density'. Where with solids, a point is either in (1) or out (0) of it, with densities, the "in-ness" of a point can assume any integer value. The gradient of density is where densities changes from x to y, supposes that the surface has a density of the difference of x and y. The 'out vector' points to an space of lower density (ie outwards).
The across or transverse out-vector exists entirely inside the surface. Since the polytope has a density, so does its surface, and in order to maintain a complete density structure, the density of the surface element must be equal to the outvector crossing it.
COMPLETE
A complete geometry has complete lines. That is, all points of the line are accessible as in a sphere. The partition of the spheric geometry into elliptic and spheric is a result that both orientability (this side of the line or that) and single-crossing (lines cross only at one point), can not both happen at once if the geometry is complete.
MAPS
small map-like surfaces, like the boy's surface, etc, do not fall specifically to any of the geometries, since they do not exist as iso-curves (circles, spheres etc). Instead, they may be regarded as modular representation of these surfaces, if the corners of each nature (vertex, edge, etc), add up to a full sphere.
THE POINT U.
There is a conformal, or angle-preserving geometry which can be transferred to any other geometry, which shows us that if any one of the geometries is valid, so are all of them. These have particular circles representing straight lines.
S For a given circle, a straight line passes through diametrically opposite points. (stereographic)
E All circles through a point represent straight lines (inversion)
H All straight lines cross a circle at right angles.
When the circle is drawn S2, (a sphere-surface), circles on the sphere then might be constructed as the crossing of the S2 and an E2 in E3. That is, a sphere intersected by planes. The conditions above then can be replaced by a single condition: whether the plane defining the plane contains a specific point 'u', which is variously inside (S), on the surface (E) or outside (H) of the sphere S2.
The relevant projective geometries can be created by adding a plane M, (map), which does not contain the point U. Because all straight lines are planes passing through U, intersect M in a line too, we see that straight lines become straight lines, but angles are lost.
S The projection through the centre of a sphere gives the azithmal projection.
E This gives the projective plane, when U is not directly opposite M, and nature when the ray perpendicular to U is perpendicular to M.
H This gives the beltrami-klein projection.
MARGINOIDS etc
=============
The surface of Thah has the properties associated with the elliptic surface, the S. version of RP2. So do a number of different figures. The polytope of 11 faces hight {3,5,3}, has vertices that are projective versions of the dodecahedron, and faces that are projective icosahedra. Still, it does not live in RP2, since the points of RP2 are to be taken as essentially homogeneous, and having points of different nature are not allowed.
Since one can cover a surface in mS etc, one can then have to deal with something that has an apparent volume, but the surface "reverses" when it crosses itself. Since there is no margin (here, edge) at the point, it is a fake margin (ie marginoid), and askew means to rotate around the margin, so the surface points up on one side and down on the other side.
The projective plane does not necessarily treat U as special: that is, the rules that give rise in RP2 applies to all geometries, until one introduces the position of the point U. It is then that RP2 divides into the three geometries (elliptic, euclidean, hyperbolic), against the conformal (spheric, euclidean, hyperbolic).
When U lies inside the sphere, the ray through U to M passes through two real points (since in S, all points are real). This means that any point in RP2 represents two real points (which is why one hears of a 'pencil' or line through the sphere). Because the notion that two lines cross at only one point holds in a fragment of euclidean geometry is transferred to all geometries, one then has the elliptic geometry a point represents actually a dipole, which in every case will fall either on the line, or on both sides of the line.
When U is on the sphere, the lines still pass through two points of the sphere, but one of these points is U. Two lines cross at U and some non-U point, in every case. The fragment denies the approachability of U, so all lines cross once.
In the case where U lies outside the sphere, a ray crosses the sphere either once (on the bounding circle), or twice. However, for a point on one side of the sphere, it is not possible to cross the boundary (which is at ever-large distances), and thus there is only one real point on the ray through U: this means that a point on M is a single point. The boundary is the base of a cone whose apex is U, crosses M in a conic.
When surfaces are allowed to cross, the solid nature of figures is replaced by the notion of 'density'. Where with solids, a point is either in (1) or out (0) of it, with densities, the "in-ness" of a point can assume any integer value. The gradient of density is where densities changes from x to y, supposes that the surface has a density of the difference of x and y. The 'out vector' points to an space of lower density (ie outwards).
The across or transverse out-vector exists entirely inside the surface. Since the polytope has a density, so does its surface, and in order to maintain a complete density structure, the density of the surface element must be equal to the outvector crossing it.
COMPLETE
A complete geometry has complete lines. That is, all points of the line are accessible as in a sphere. The partition of the spheric geometry into elliptic and spheric is a result that both orientability (this side of the line or that) and single-crossing (lines cross only at one point), can not both happen at once if the geometry is complete.
MAPS
small map-like surfaces, like the boy's surface, etc, do not fall specifically to any of the geometries, since they do not exist as iso-curves (circles, spheres etc). Instead, they may be regarded as modular representation of these surfaces, if the corners of each nature (vertex, edge, etc), add up to a full sphere.
THE POINT U.
There is a conformal, or angle-preserving geometry which can be transferred to any other geometry, which shows us that if any one of the geometries is valid, so are all of them. These have particular circles representing straight lines.
S For a given circle, a straight line passes through diametrically opposite points. (stereographic)
E All circles through a point represent straight lines (inversion)
H All straight lines cross a circle at right angles.
When the circle is drawn S2, (a sphere-surface), circles on the sphere then might be constructed as the crossing of the S2 and an E2 in E3. That is, a sphere intersected by planes. The conditions above then can be replaced by a single condition: whether the plane defining the plane contains a specific point 'u', which is variously inside (S), on the surface (E) or outside (H) of the sphere S2.
The relevant projective geometries can be created by adding a plane M, (map), which does not contain the point U. Because all straight lines are planes passing through U, intersect M in a line too, we see that straight lines become straight lines, but angles are lost.
S The projection through the centre of a sphere gives the azithmal projection.
E This gives the projective plane, when U is not directly opposite M, and nature when the ray perpendicular to U is perpendicular to M.
H This gives the beltrami-klein projection.
MARGINOIDS etc
=============
The surface of Thah has the properties associated with the elliptic surface, the S. version of RP2. So do a number of different figures. The polytope of 11 faces hight {3,5,3}, has vertices that are projective versions of the dodecahedron, and faces that are projective icosahedra. Still, it does not live in RP2, since the points of RP2 are to be taken as essentially homogeneous, and having points of different nature are not allowed.
Since one can cover a surface in mS etc, one can then have to deal with something that has an apparent volume, but the surface "reverses" when it crosses itself. Since there is no margin (here, edge) at the point, it is a fake margin (ie marginoid), and askew means to rotate around the margin, so the surface points up on one side and down on the other side.
The projective plane does not necessarily treat U as special: that is, the rules that give rise in RP2 applies to all geometries, until one introduces the position of the point U. It is then that RP2 divides into the three geometries (elliptic, euclidean, hyperbolic), against the conformal (spheric, euclidean, hyperbolic).
When U lies inside the sphere, the ray through U to M passes through two real points (since in S, all points are real). This means that any point in RP2 represents two real points (which is why one hears of a 'pencil' or line through the sphere). Because the notion that two lines cross at only one point holds in a fragment of euclidean geometry is transferred to all geometries, one then has the elliptic geometry a point represents actually a dipole, which in every case will fall either on the line, or on both sides of the line.
When U is on the sphere, the lines still pass through two points of the sphere, but one of these points is U. Two lines cross at U and some non-U point, in every case. The fragment denies the approachability of U, so all lines cross once.
In the case where U lies outside the sphere, a ray crosses the sphere either once (on the bounding circle), or twice. However, for a point on one side of the sphere, it is not possible to cross the boundary (which is at ever-large distances), and thus there is only one real point on the ray through U: this means that a point on M is a single point. The boundary is the base of a cone whose apex is U, crosses M in a conic.
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2014
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
Re: Question regarding the real projective plane
Yet another attempt in rendering the projective plane

Left: Transparent version to see interior structure of the 3D model
Right Opaque structure
I call this the projective plum since this particular model looks like a plum being sliced open with the inner dome act as the "stone"
This plum is constructed by folding the moebius strip so that the left half ( original boundary shaped like a "G") coincides with the right half (shaped like a mirror reversed G)
Non Orientablility Test
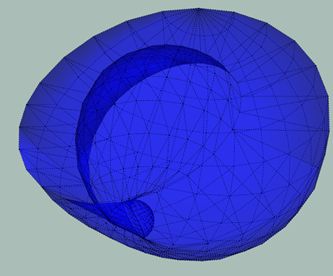
To be non orientable means there is only one side. In other words when I paint this thing, I should be able to paint the whole thing including the "inside" in just one color
Therefore the plum passes this test
Genus Zero Test
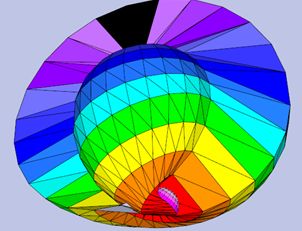
Here I colored the simplest example of the orientable loops. The loops will vanish into a point when they moved towards the black band. They can get nowhere if they tried to travel to the pink hemisphere end (details below)
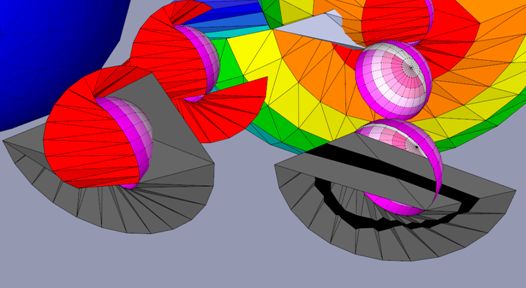
Above are the fragments isolated from the main thing to give a clearer view on what happen if I take an orientable loop (Top row) and a non orientable loop (Bottom row) and test them
Orientable loop going towards the hemisphere (presumably the Mrrl Test)
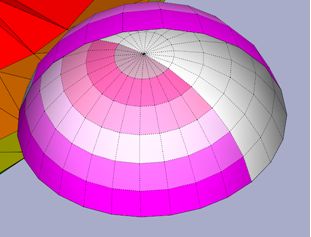
As the red loop slide into the hemisphere, one half enters the "inner side" and another enters the "outer side" of the hemisphere. Although I did not color it completely for the sake of clarity, you can notice both sides of the pink region are of the same color (since you can slide the halves of the loop around the hemisphere so that it covers the entire "inner/outer" side of the hemisphere). This is only possible in this hemispherical region (The "inner" side of the other bands are white as they remained uncolored). If my interpretation is right then this might be the "last ring is a neighbour of itself" that Mrrl is referring to.
In fact the circular rim (and the moebius strip the cross through the circle) is where the inversion region (the region where it is allowed to turn inside out) or to put it in Wendy's term: Askew Marginoid is located on this plum
Now if you slide the loop further...
eventually the outer and inner half of the loop coincide and form the arc as shown (projective line of the plane???). You can then notice how it got hinged by the rim of the hemisphere and this explains why it (and possiblity any orientable loop) cannot be shrank to a point in the hemispherical side
Non orientable loop unshrankable test
Here I choose a non orientable loop to test its unshrankability. In fact, the above case also implictly illustrates a non orientable loop with get hinged at the circular rim.
Then you might ask, what if we take one part of the loop slide it around the red band so that it slide along the hemisphere and eventually untangle and shrink away? (refer to the fragements pics above cause this pics I cut away the band for the sake of clarity) . This is actually the most difficult test to carry out, but preliminary result shows that at least one portion of the loop will still get stuck at the striaght portion of the grey band (i.e. get hinged by the rim of the hemisphere) even if you tried pulling the loop around the red band (refer toi fragement pics, not shown here). Therefore i cannot get untangled and cannot shrink into a point.
Then you might ask, what about pulling the loop towards the black end?. The results is no as when you are pulling the loop around, you are extending the loop portions along the broad region of the plum

Therefore they will be at least one portion of the loop remain stuck at the broad region and cannot be pulled back to the black end and shrink to a point.
As a result the plum pass the Genus Zero (and presumably the Mrrl Test)
Connected sum test
1. Moebius strip after chopping a disk away?

Notice I have now chopped away the disk (a hemisphere is homeomorphic to a disk i.e. you can deform a hemisphere into a filled in circle). From the results of the Non Orientablility test, the surface remains non orientable yet it now has a circular boundary. The pulm have now become a moebius stripe (It is not homeomorphic to a Sudanese moebius strip however as this model crosses itself near the circular edge)
Therefore the plum passes the 1st stage
2. Test for klein bottle

Maths told us that if we connect two RP2 together at the circular end after chopping away the disks (i.e. RP2#RP2), the result is a klein bottle. To be a klein bottle one must be
Genus 1 and non orientable
Here it shows that I can paint the whole thing green in one stroke, thus the object is non orientable
Now to check its genus
To be genus one it means there is at least one orientable loop cannot be shrinked into a point. Here I choose an extreme sample of a orientable loop (The inversion region is always located at the circular area where the two chopped plums met, thus any other orientable loop that spans the whole shape must pass through this region, thus proving the red loop cannot be shrinked also prove other loops cannot be shirnked). On the right side is the loop being isolated. I then untangle the loop carefully to show it is homeomorphic to a circle (top figure of right pics). As it canot receed away from the circular region to shrink, it means this loop is hinged at this circle (the neck of the klein bottle). Therefore I've proved that this surface is genus 1
As a result the plum passes the connected sum test
Therefore it is VERY LIKELY (because of the non oreintable loop issue which is difficult to test) to be a real projective plane
However I think this plum is not really that beautiful as you can still see it crosses through itself many times, though it does not have pinch points nor it has 3 fold symmetry as the boy's surface (thus less confusing as you don't need to loop around thrice to be non orientable)
IMO only a capped Sudanese moebius strip will look better and easier to understand
Problem is I don't have the instructions to fold a Sudanese moebius stripe

Left: Transparent version to see interior structure of the 3D model
Right Opaque structure
I call this the projective plum since this particular model looks like a plum being sliced open with the inner dome act as the "stone"
This plum is constructed by folding the moebius strip so that the left half ( original boundary shaped like a "G") coincides with the right half (shaped like a mirror reversed G)
Non Orientablility Test

To be non orientable means there is only one side. In other words when I paint this thing, I should be able to paint the whole thing including the "inside" in just one color
Therefore the plum passes this test
Genus Zero Test

Here I colored the simplest example of the orientable loops. The loops will vanish into a point when they moved towards the black band. They can get nowhere if they tried to travel to the pink hemisphere end (details below)

Above are the fragments isolated from the main thing to give a clearer view on what happen if I take an orientable loop (Top row) and a non orientable loop (Bottom row) and test them
Orientable loop going towards the hemisphere (presumably the Mrrl Test)

Mrrl wrote:[...]But you also need that the last ring is a neighbour of itself, like "halves" of Moebius stripe, and its outside boundary should be a non-orientable curve ("projective line" of the plane) - with the same color on both sides. If your painting has these properties, than yes, the surface is a projective plane. [...]
As the red loop slide into the hemisphere, one half enters the "inner side" and another enters the "outer side" of the hemisphere. Although I did not color it completely for the sake of clarity, you can notice both sides of the pink region are of the same color (since you can slide the halves of the loop around the hemisphere so that it covers the entire "inner/outer" side of the hemisphere). This is only possible in this hemispherical region (The "inner" side of the other bands are white as they remained uncolored). If my interpretation is right then this might be the "last ring is a neighbour of itself" that Mrrl is referring to.
In fact the circular rim (and the moebius strip the cross through the circle) is where the inversion region (the region where it is allowed to turn inside out) or to put it in Wendy's term: Askew Marginoid is located on this plum
Now if you slide the loop further...

eventually the outer and inner half of the loop coincide and form the arc as shown (projective line of the plane???). You can then notice how it got hinged by the rim of the hemisphere and this explains why it (and possiblity any orientable loop) cannot be shrank to a point in the hemispherical side
Non orientable loop unshrankable test

Here I choose a non orientable loop to test its unshrankability. In fact, the above case also implictly illustrates a non orientable loop with get hinged at the circular rim.
Then you might ask, what if we take one part of the loop slide it around the red band so that it slide along the hemisphere and eventually untangle and shrink away? (refer to the fragements pics above cause this pics I cut away the band for the sake of clarity) . This is actually the most difficult test to carry out, but preliminary result shows that at least one portion of the loop will still get stuck at the striaght portion of the grey band (i.e. get hinged by the rim of the hemisphere) even if you tried pulling the loop around the red band (refer toi fragement pics, not shown here). Therefore i cannot get untangled and cannot shrink into a point.
Then you might ask, what about pulling the loop towards the black end?. The results is no as when you are pulling the loop around, you are extending the loop portions along the broad region of the plum

Therefore they will be at least one portion of the loop remain stuck at the broad region and cannot be pulled back to the black end and shrink to a point.
As a result the plum pass the Genus Zero (and presumably the Mrrl Test)
Connected sum test
1. Moebius strip after chopping a disk away?

Notice I have now chopped away the disk (a hemisphere is homeomorphic to a disk i.e. you can deform a hemisphere into a filled in circle). From the results of the Non Orientablility test, the surface remains non orientable yet it now has a circular boundary. The pulm have now become a moebius stripe (It is not homeomorphic to a Sudanese moebius strip however as this model crosses itself near the circular edge)
Therefore the plum passes the 1st stage
2. Test for klein bottle

Maths told us that if we connect two RP2 together at the circular end after chopping away the disks (i.e. RP2#RP2), the result is a klein bottle. To be a klein bottle one must be
Genus 1 and non orientable
Here it shows that I can paint the whole thing green in one stroke, thus the object is non orientable
Now to check its genus

To be genus one it means there is at least one orientable loop cannot be shrinked into a point. Here I choose an extreme sample of a orientable loop (The inversion region is always located at the circular area where the two chopped plums met, thus any other orientable loop that spans the whole shape must pass through this region, thus proving the red loop cannot be shrinked also prove other loops cannot be shirnked). On the right side is the loop being isolated. I then untangle the loop carefully to show it is homeomorphic to a circle (top figure of right pics). As it canot receed away from the circular region to shrink, it means this loop is hinged at this circle (the neck of the klein bottle). Therefore I've proved that this surface is genus 1
As a result the plum passes the connected sum test
Therefore it is VERY LIKELY (because of the non oreintable loop issue which is difficult to test) to be a real projective plane
However I think this plum is not really that beautiful as you can still see it crosses through itself many times, though it does not have pinch points nor it has 3 fold symmetry as the boy's surface (thus less confusing as you don't need to loop around thrice to be non orientable)
IMO only a capped Sudanese moebius strip will look better and easier to understand
Problem is I don't have the instructions to fold a Sudanese moebius stripe
- Secret
- Trionian
- Posts: 162
- Joined: Tue Jul 06, 2010 12:03 pm
Re: Question regarding the real projective plane
Wow. Most of this discussion went way over my head. One of these days I really have to sit down and start working with 2-manifolds immersed in 4D -- I have mastered the basics of 4D visualization of 3-manifolds to some extent, but I've to admit the 2-manifolds are still beyond me. The only thing I've gotten down pat is the Klein bottle. I've tried on various occasions to tackle RP2 but I found that 3D immersions of it just does not work for me; what I need is a direct 4D immersion to work with. Except that people don't usually use 4D illustrations for explaining RP2. 

- quickfur
- Pentonian
- Posts: 2955
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
20 posts
• Page 1 of 1
Who is online
Users browsing this forum: No registered users and 22 guests
